2. Tutorial Avanzado

En esta parte del tutorial aprenderá a utilizar Python para manejar vectores y matrices, crear gráficas y resolver integrales. Estas funciones serán trascendentales para el curso de Química Cuántica. Recuerde escribir en los cuadros vacíos y presionar el botón Run o las teclas “Shift” + “Enter”.

Utilizaremos las librerías numpy, matplotlib y scipy que aprendió a utilizar en el Tutorial Básico, impórtelas en el siguiente recuadro.

# Importe librerías

import numpy as np
from matplotlib import pyplot as plt
import scipy

2.1. Vectores y Matrices

Python permite manejar fácilmente objetos multidimensionales, como vectores y matrices.

Aprendizaje de código

Empezaremos creando una lista, la cual es un conjunto de cosas. Las listas se crean poniendo elementos entre corchetes cuadrados, por ejemplo

lista = [5, 9, 4]

Podemos imprimir todos los elementos de la lista con

print(lista)

También podemos imprimir un elemento específico indicando el número del elemento entre paréntesis cuadrados. En Python los elementos se cuentan desde “cero”. Para imprimir el número 9 en la lista anterior ejecutaríamos:

print(lista[1])

Cree la siguiente lista [8,25,32,41] y guárdela en la variable “lista”. Imprima la lista completa, así como el primer elemento del vector.

#Cree una lista

lista = [8,25,32,41]
print(lista)
print(lista[0])

[8, 25, 32, 41]
8

La lista puede convertirse en un arreglo de numpy, esto facilita el manejo de cantidades vectoriales.

Aprendizaje de código

Para declarar la lista anterior como un arreglo de numpy escribiremos

vector = np.array([5, 9, 4])

Una ventaja es que podemos declarar dos arreglos, por ejemplo

v1 = np.array([2, 4, 6])
v2 = np.array([3, 5, 7])

y sumarlos, de una forma muy parecida a como se haría en física.

print(v1+v2)

Cree dos vectores como arreglos de numpy, uno que contenga los elementos “1,8,6”, y otro que contenga “5,2,7”, e imprima su suma

#Suma de dos vectores

v1 = np.array([1,8,6])
v2 = np.array([5,2,7])

print(v1+v2)

[ 6 10 13]

Aprendizaje de código

También podemos crear matrices como una “lista de listas”, donde cada lista representa un renglón de la matriz. A continuación generemos una matriz de 3x3 que contenga ceros en todos sus elementos

matriz = [[0.0, 0.0, 0.0],[0.0, 0.0, 0.0],[0.0, 0.0, 0.0]]

Genere la matriz de ceros anterior, e imprímala.

#Cree matriz

Aprendizaje de código

Podemos usar numpy para hacer nuestra matriz de ceros de forma más fácil

matriz = np.zeros((3,3))
print(matriz)

Prueba usar numpy para definir una matriz de ceros de 5x5, e imprímala.

#Cree matriz de ceros con numpy

matriz = np.zeros((5,5))
print(matriz)

[[0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]]

A continuación genere una matriz de 3x3, guárdela en la variable “matriz1”, y asígnele los valores del 1 al 9, tal que

\[\begin{split} \text{matriz}1 = \begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ \end{pmatrix} \end{split}\]

Puede ayudarse del siguiente código.

matriz1 = np.zeros((3,3))
matriz1[0][0]=1.0
matriz1[0][1]=2.0
matriz1[0][2]=3.0
matriz1[1][0]=4.0
matriz1[1][2]=5.0
...

#Llene una matriz de 3x3

matriz1 = np.zeros((3,3))
matriz1[0][0]=1.0
matriz1[0][1]=2.0
matriz1[0][2]=3.0
matriz1[1][0]=4.0
matriz1[1][1]=5.0
matriz1[1][2]=6.0
matriz1[2][0]=7.0
matriz1[2][1]=8.0
matriz1[2][2]=9.0

Aprendizaje de código

Hacer esto puede tomar mucho tiempo con matrices grandes. Existe una instrucción llamada for que nos permite hacer cosas repetitivas. Por ejemplo:

matriz2 = np.zeros((3,3))
val=0.0
for i in range(3):
    for j in range(3):
        val=val+1.0
        matriz2[i][j]=val

Prueba la instrucción anterior e imprime las dos matrices (matriz1 y matriz2) en el siguiente recuadro.

#Matriz de 3x3 con for

Aprendizaje de código

Se pueden multiplicar dos matrices con

matriz3=np.matmul(matriz1,matriz2)

Multiplique las dos matrices anteriores e imprima el resultado.

#Matriz3 = Matriz1 x Matriz2

Los valores propios (\(\lambda\)) y vectores propios (\(v\)) de una matriz (\(M\)) son muy importantes en química cuántica. Cumplen la propiedad de que al multiplicar la matriz por el vector propio resulta el mismo vector multiplicado por una constante, es decir:

\[ M v = \lambda v \]

Aprendizaje de código

Los valores y vectores propios se pueden calcular con

val,vec=np.linalg.eig(matriz)

Calcule los valores propios y vectores propios de la matriz 1, e imprímalos.

Si la matriz es simétrica o hermitiana es más conveniente usar np.linalg.eigh(matriz).

np.linalg.eig(matriz) regresa valores propios desordenados mientras que np.linalg.eigh(matriz) los regresa ordenados.

# Valores y vectores propios

val,vec=np.linalg.eig(matriz1)

2.2. Gráficas

Vamos a graficar la función \(y=\sin(x)\) de \(-3\) a \(3\).

Aprendizaje de código

Primero crearemos el dominio de la función (los valores de x), en nuestro ejemplo le daremos 50 puntos. Utilizaremos la función linspace(a,b,n) de numpy, esta crea un conjunto de n números distribuidos en el intervalo de a hasta b.

x=np.linspace(-3,3,50)

Genere el dominio tal que \(x\in[-3,3]\), utilice 50 puntos, guárdelo en la variable x e imprímalo.

# Cree dominio de x

Aprendizaje de código

Obtendremos el valor de “y” usando numpy. Al escribir la siguiente instrucción Python toma cada valor de x, le aplica la función y lo guarda en la variable “y”.

y=np.sin(x)

Evalúe la función

\[ y = \sin(x) \]

# Evalúe función

Aprendizaje de código

Finalmente, realice la gráfica con

plt.scatter(x,y)
plt.show()

Prueba cambiar plt.scatter(x,y) por plt.plot(x,y) para tener una gráfica continua.

# Genere gráfica

from matplotlib import pyplot as plt
import numpy as np

x=np.linspace(-3,3,50)
y=np.sin(x)

plt.scatter(x,y)
#plt.plot(x,y)
plt.show()

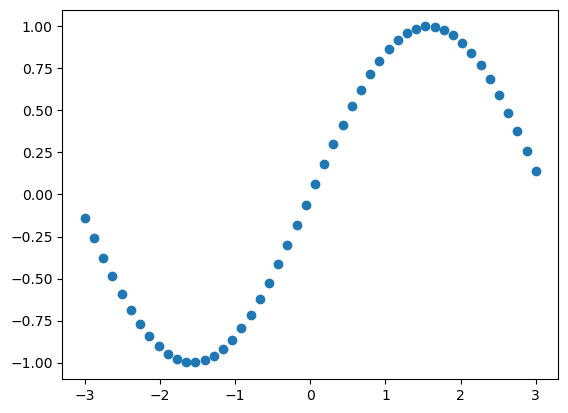
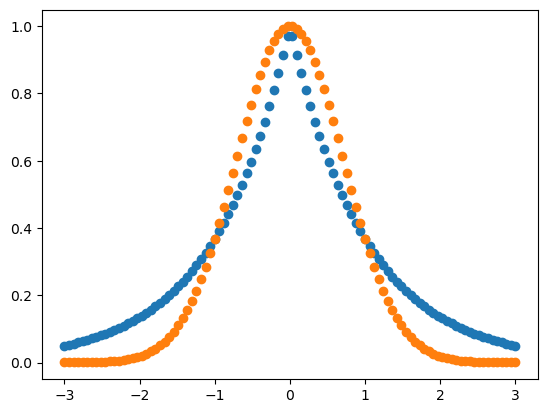
Las instrucciones anteriores son los pasos básicos para generar una gráfica. En el siguiente recuadro genere la gráfica de las funciones \(y_1=e^{-|x|}\) y \(y_2=e^{-|x|^2}\) con 100 puntos desde -3 hasta 3.

# Gráfica

x  = np.linspace(-3,3,100)
y1 = np.exp(-np.abs(x))
y2 = np.exp(-np.abs(x)**2)

plt.scatter(x,y1)
plt.scatter(x,y2)

plt.show()

2.3. Integrales

Aprendizaje de código

También podemos hacer integrales con Python. Por ejemplo, vamos a integrar \(y=x^2\) en el dominio \(-3 \leq x \leq 3\). Para ello importaremos el subpaquete integrate de la librería scipy.

from scipy import integrate

y luego realizaremos la integral con la función quad

integrate.quad(lambda x: x**2,-3,3)[0]

Aquí “lambda” indica las variables de la ecuación, seguido de la ecuación y los límites de la integral.

El resultado de integrate.quad es un vector, por eso al final de la línea escribimos [0] para acceder al primer elemento, que contiene el resultado de la integral. Pruebe escribiendo integrate.quad(lambda x: x**2,-3,3) y observe la diferencia.

Pruebe a realizar la integral.

# Integre y = x**2 de -3 a 3

import scipy.integrate as integrate
integrate.quad(lambda x: x**2,-3,3)[0]

18.0

Considere la función de onda \(\psi = x\), con \(x \epsilon [-3,3]\), proponga una función de onda normalizada y evalúe la integral con integrate.quad para comprobar que la norma es 1.

Tip

Recuerde que para normalizar:

1 Integre el cuadrado de la función de onda en el dominio.

\[ N^2 = \int_{x_1}^{x_2} |\psi_ {\rm original}|^2 dr \]

2 Obtenga la norma.

\[ N = \sqrt{N^2} = \sqrt{\int_{x_1}^{x_2} |\psi_{\rm original}|^2 dx} \]

3 Multiplique la función de onda original por el inverso de su norma.

\[ \psi_{\rm normalizada} = \frac{1}{N} \psi_{\rm original} \]

#Normalice función de onda

norm2 = integrate.quad(lambda x: x*x,-3,3)[0]
print("N**2 =",norm2)

norm = np.sqrt(norm2)
print("N =",norm)

integrate.quad(lambda x: (x/norm)*(x/norm),-3,3)[0]

N**2 = 18.0
N = 4.242640687119285

1.0

OPCIONAL

Aprendizaje de código

También es posible realizar integrales triples, el siguiente ejemplo solo es demostrativo, simplemente copie y pegue para realizar la integral.

Sea la función de onda

\[ \psi = e^{-(x^2+y^2+z^2)}=e^{-r^2} \]

La integral de su cuadrado será

\[\begin{eqnarray*} N^2 &=& \int \bigg( \psi^* \psi \bigg)\,d\textbf{r} = \int\limits_{0}^\pi \int\limits_{0}^{2\pi} \int\limits_{0}^\infty \bigg(\psi^* \psi\, r^2 \sin\theta \bigg) dr d\phi d\theta \\ &=& \int\limits_{0}^{\pi} \sin \theta d\theta \int\limits_{0}^{2\pi} d\phi \int\limits_{0}^\infty e^{-2r^2} r^2 dr \\ &=& \left(2\pi\right)\left(2\right)\left(\frac{1}{8}\sqrt{\frac{\pi}{2}}\right) = \left(\frac{\pi}{2}\right)^{3/2} \end{eqnarray*}\]

El siguiente código evalúa la integral y la guarda en la variable “norm2”.

norm2 = integrate.tplquad(lambda theta,phi,r: r**2.0*np.sin(theta)*np.exp(-2.0*r**2.0), 0, np.inf, lambda r: 0, lambda theta: 2*np.pi,lambda r, theta: 0, lambda r, theta: np.pi)[0]

Nuestro objetivo en este punto es que conozca lo mucho que se puede hacer en Python. Exploraremos estas ideas más adelante.

#Determine el cuadrado de la norma de la función de onda

norm2 = integrate.tplquad(lambda theta,phi,r: r**2.0*np.sin(theta)*np.exp(-2.0*r**2.0), 0, np.inf, lambda r: 0, lambda theta: 2*np.pi,lambda r, theta: 0, lambda r, theta: np.pi)[0]

print("N**2 =",norm2)

N**2 = 1.968701243215302

Compruebe que numéricamente esto es \(\left(\frac{\pi}{2}\right)^{3/2}\).

#Evalúe (pi/2)^(3/2)

print((np.pi/2)**(3/2))

1.9687012432153024

Evalúe la norma

# Constante de normalización

norm = np.sqrt(norm2)
print("N =",norm)

N = 1.403104145534216

OPCIONAL

Proponga una \(\psi\) normalizada, y compruebe que la integral de su cuadrado da 1. Recuerde la siguiente relación

\[ \psi_{\rm normalizada} = \frac{1}{\sqrt{N}} \psi_{\rm original} \]

y que para este ejercicio

\[ \psi_{\rm original} = e^{-r} \]

#Comprobación

norm = integrate.tplquad(lambda theta,phi,r: 1/norm**2*r**2.0*np.sin(theta)*np.exp(-2.0*r**2.0), 0, np.inf, lambda r: 0, lambda theta: 2*np.pi,lambda r, theta: 0, lambda r, theta: np.pi)[0]
print(norm)

1.0

OPCIONAL

Repita el proceso de normalización para \(\psi=re^{-r^2}\). La integral sin normalizar será

\[ \int \psi^* \psi \,d\textbf{r} = \frac{3}{4}\left(\frac{\pi}{2}\right)^{3/2} \]

#Normalice

norm2=integrate.tplquad(lambda theta,phi,r: r**4.0*np.sin(theta)*np.exp(-2.0*r**2.0), 0, np.inf, lambda r: 0, lambda theta: 2*np.pi,lambda r, theta: 0, lambda r, theta: np.pi)[0]
print("N**2 =",norm2)

norm = np.sqrt(norm2)
print("N =",norm)

norm=integrate.tplquad(lambda theta,phi,r: 1/norm**2*r**4.0*np.sin(theta)*np.exp(-2.0*r**2.0), 0, np.inf, lambda r: 0, lambda theta: 2*np.pi,lambda r, theta: 0, lambda r, theta: np.pi)[0]
print(norm)

N**2 = 1.4765259324114768
N = 1.2151238341878892

1.0