10. Oscilador Armónico Cuántico#

El sistema es una partícula que se mueve en un potencial dado por

\[ V = \frac{1}{2} kx^2 \]

donde \(k\) es una constante.

Note

En mecánica clásica podemos encontrar sistemas con este potencial como los resortes, mientras que en química cuántica esto sirve para modelar la vibración de los enlaces.

En este caso, el Hamiltoniano contiene la energía cinética y el potencial

\[ H = -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2} kx^2 \]

y la ecuación de Schrödinger a resolver es

\[ \left(-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2} kx^2 \right) \psi = E \psi \]

esta es una ecuación cuyas soluciones a la energía y las eigenfunciones son

\[ E_n = \left(n + \frac{1}{2}\right) h \nu \]
\[ \psi_n = N_n H_n(\alpha x) e^{-\alpha^2x^2/2} \]

aquí \(n\) es un número cuántico tal que \(n = 0,1,2,3,...\), y los términos \(N_n\) y \(\alpha\) están dados por

\[ N_n = \left(\frac{\alpha}{2^n n! \pi^{1/2}} \right)^{1/2} \]
\[ \alpha = \left( \frac{mk}{\hbar^2} \right)^{1/4} \]

\(H_n(x)\) son los polinomios de Hermite

\(n\)

\(H_n(x)\)

0

\(1\)

1

\(2x\)

2

\(4x^2 -2\)

3

\(8x^3 - 12 x\)

4

\(16x^4 - 48 x^2 +12\)

10.1. Gráficas de las eigenfunciones#

Importe las librerías numpy, math, pyplot de matplotlib y eval_hermite de scipy.special

# Importe librerías

import numpy as np
import math
from matplotlib import pyplot as plt
from scipy.special import eval_hermite

Asigne valores a las constantes \(m\), \(k\), \(\hbar\), \(h\), \(\alpha\). Considere \(m=1\), \(k=1\), \(\hbar=1\).

# Asigne valores

m=1.0
k=1.0
hbar=1.0
h = hbar*2*np.pi

alpha = np.power(m*k/(hbar**2),1/4)

Defina un dominio de puntos para x, por ejemplo \(1000\) puntos de \(-5\) a \(5\).

# Defina dominio

x = np.linspace(-5,5,1000)

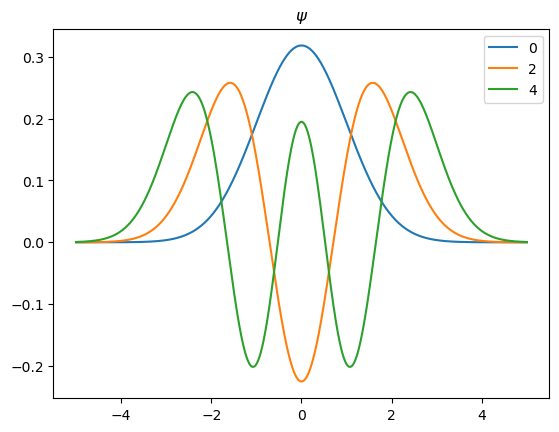
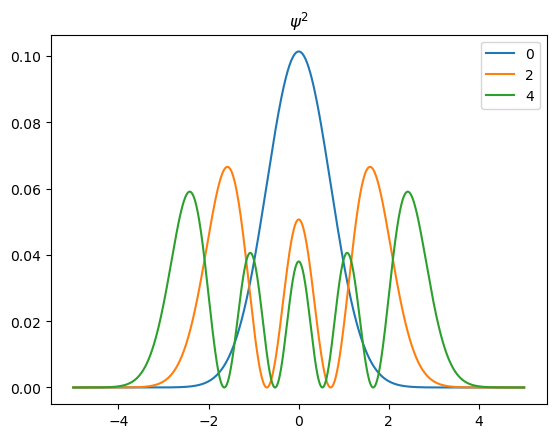
Grafique la eigenfunción del oscilador Harmónico cuántico y su cuadrado para \(n=0,2,4\).

Compare con Atkins, P. W.; Friedman, R. Molecular Quantum Mechanics, 4th ed.; Oxford University Press: New York, 2005, p.62.

# Gráfica

#Psi
for n in range(0,5,2):
    N_n = np.sqrt(alpha/(2**n*math.factorial(n)*np.pi**2))
    H_n = eval_hermite(n,alpha*x)
    psi_n = N_n*H_n*np.exp(-alpha**2*x**2/2)
    plt.plot(x,psi_n,label=n)
plt.legend()
plt.title("$\psi$")
plt.show()

#Psi^2
for n in range(0,5,2):
    N_n = np.sqrt(alpha/(2.0**n*math.factorial(n)*np.pi**2))
    H_n = eval_hermite(n,alpha*x)
    psi_n = N_n*H_n*np.exp(-alpha**2*x**2/2)
    plt.plot(x,psi_n**2,label=n)
plt.legend()
plt.title("$\psi^2$")
plt.show()
_images/Oscilador_14_0.png _images/Oscilador_14_1.png

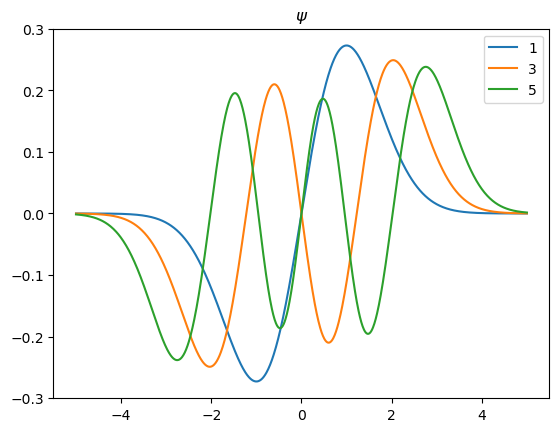
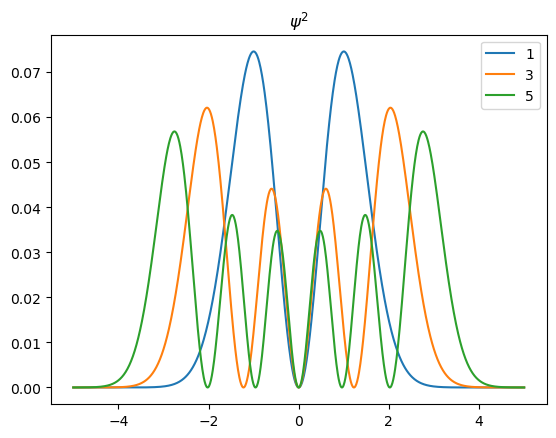
Grafique la eigenfunción del oscilador Harmónico cuántico para \(n=1,3,5\).

Compare con Atkins, P. W.; Friedman, R. Molecular Quantum Mechanics, 4th ed.; Oxford University Press: New York, 2005, p.62.

# Gráfica

#Psi
for n in range(1,6,2):
    N_n = np.sqrt(alpha/(2**n*math.factorial(n)*np.pi**2))
    H_n = eval_hermite(n,alpha*x)
    psi_n = N_n*H_n*np.exp(-alpha**2*x**2/2)
    plt.plot(x,psi_n,label=n)
plt.legend()
plt.title("$\psi$")
plt.show()

#Psi^2
for n in range(1,6,2):
    N_n = np.sqrt(alpha/(2**n*math.factorial(n)*np.pi**2))
    H_n = eval_hermite(n,alpha*x)
    psi_n = N_n*H_n*np.exp(-alpha**2*x**2/2)
    plt.plot(x,psi_n**2,label=n)
plt.legend()
plt.title("$\psi^2$")
plt.show()
_images/Oscilador_17_0.png _images/Oscilador_17_1.png

10.2. Valores Esperados#

A continuación calcularemos valores esperados correspondientes al estado basal. Para ello importe el módulo de integración de scipy.

# Improte integrate de scipy

from scipy import integrate
\[\newcommand{\expval}[1]{\left\langle{#1}\right\rangle}\]

Calcule el valor esperado de la posición, es decir, realice la integral

\[\begin{equation*} \expval{x} = \int_{-\infty}^{\infty} \psi^* x \psi dx \end{equation*}\]
# Realice la integral

n = 0
N_n = np.sqrt(alpha/(2**n*math.factorial(n)*np.pi**2))

integrate.quad(lambda x: N_n*eval_hermite(n,alpha*x)*np.exp(-alpha**2*x**2/2) * (x) * N_n*eval_hermite(n,alpha*x)*np.exp(-alpha**2*x**2/2),-np.inf,np.inf)[0]

0.0

Calcule el valor esperado del cuadrado de la posición, es decir, realice la integral

\[\begin{equation*} \expval{x^2} = \int_{-\infty}^{\infty} \psi^* x^2 \psi dx \end{equation*}\]
# Realice la integral

n = 0
N_n = np.sqrt(alpha/(2**n*math.factorial(n)*np.pi**2))

integrate.quad(lambda x: N_n*eval_hermite(n,alpha*x)*np.exp(-alpha**2*x**2/2) * (x**2) * N_n*eval_hermite(n,alpha*x)*np.exp(-alpha**2*x**2/2),-np.inf,np.inf)[0]

0.0897935610625835

Pregunta

Considere los siguientes hechos:

  • La raíz de la desviación cuadrática media de la posición está dada por:

\[\begin{equation*} \Delta x = \sqrt{\expval{x^2} - \expval{x}^2} \end{equation*}\]

  • Considere que para este sistema \(\expval{x}=0\), y que la desviación cuadrática media del momento lineal tiene un valor finito mayor a cero, \(\Delta p_x>0\). ¿Por qué \(\expval{x^2}\) no puede ser cero en ningún caso?

Ayuda. Revise el principio de incertidumbre y el producto \(\Delta x \Delta p_x\).

Respuesta

El principio de incertidumbre establece la restricción

\[\begin{equation*} \Delta x \Delta p_x \geq \frac{1}{2}\hbar \end{equation*}\]

Por lo tanto, si \(\Delta p_x\) tiene un valor finito, entonces \(\Delta x\) no puede ser cero o se rompería el principio variacional. Ya que \(\expval{x}=0\), entonces el valor de \(\Delta x = \sqrt{\expval{x^2} - \expval{x}^2}\) está únicamente determinado por \(\expval{x^2}\) que, por tanto, tampoco puede ser cero.

10.3. Referencias#

  • T.J. Zielinski, Exploring the Harmonic Oscillator Wave Functions, J. Chem. Educ. 84, 1232 (2007).

  • J.J. Bruce y B.D. Anderson, Investigating the harmonic oscillator using Mathematica, J. Chem. Educ. 70, A122 (1993).

  • P. W. Atkins, y R. Friedman, Molecular Quantum Mechanics (Oxford University Press, 2005).