5. Penetración

Considere una partícula moviéndose hacia una barrera de potencial de longitud infinita de valor V en \(x=0\). Antes de \(x=0\) el potencial vale cero, y después vale \(V\), es decir:

\[\begin{split} V(x) = \left\{ \begin{array}{lll} 0 & \mathrm{si\ } x < 0 & \text{I}\\ V & \mathrm{si\ } 0 \le x < \infty & \text{II} \\ \end{array} \right. \end{split}\]

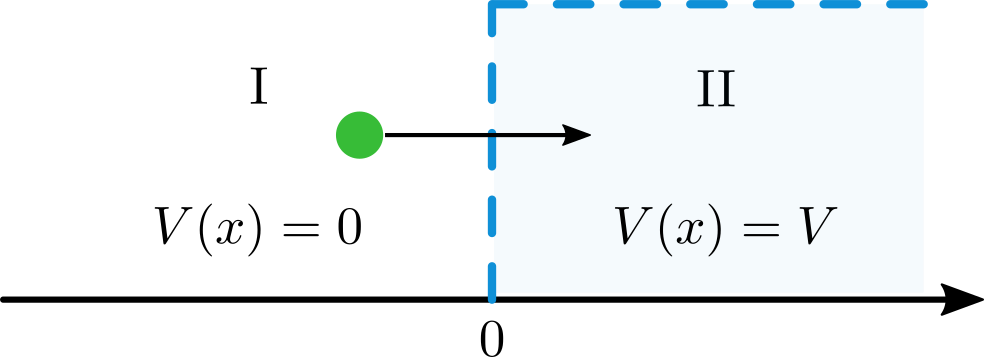
En este sistema consideraremos el caso en el que la partícula tiene menor energía, \(E\), que el potencial, \(V\), es decir, \(E < V\).

Para pensar

De manera clásica, la partícula no podría pasar del lado izquierdo (región I) al lado derecho (región II) de la caja, porque no tiene suficiente energía. Por esta razón, no podríamos encontrar a la partícula en la región II. ¿Qué pasará cuánticamente?

Para resolver el sistema hay que planear el Hamiltoniano por regiones y resolver una eigenfunción para cada región.

Inserto matemático: Hamiltoniano por regiones

Región	Hamiltoniano	Eigenfunción	Constantes
I	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)	\(\psi_{\rm I}(x) = Ae^{ikx} + Be^{-ikx}\)	\(k^2 = \frac{2mE}{\hbar^2}\)
II	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V\)	\(\psi_{\rm II}(x) = C e^{-\kappa x} + De^{\kappa x}\)	\(\kappa ^2 = \frac{2m(V-E)}{\hbar^2}\)

Se obtienen la eigenfunción por regiones

\[ \psi_I(x) = Ae^{ikx} + Be^{-ikx} \]

\[ \psi_{\rm II}(x) = C e^{-\kappa x} + De^{\kappa x} \]

Note la diferencia entre la letra k y la letra griega \(\kappa\).

Los coeficientes pueden obtenerse a partir de la condición de continuidad de la eigenfunción en \(x=0\)

Inserto matemático: Condiciones de continuidad

Regiones	Condición	Ecuación
II	\(\psi_{\rm II}(\infty) = 0\)	\(D = 0\)
I y II	\(\psi_{\rm I}(0) = \psi_{\rm II}(0)\)	\(A + B = C\)
I y II	\(\frac{\psi_{\rm I}}{dx}(0) = \frac{\psi_{\rm II}}{dx}(0)\)	\(ik (A - B) = - \kappa C\)

Se obtiene

\[ B = -\left(\frac{\kappa + ik}{\kappa - ik}\right) A \]

\[ C = \frac{2ik}{ik - \kappa} A \]

Importe numpy y pyplot de matplotlib.

# Importe librerías

import numpy as np
from matplotlib import pyplot as plt

De valores a las constantes del sistema. Considere \(m=1\), \(\hbar=1\). Asigne algún valor a la energía y al potencial, respetando que \(V > E\), observe que en este caso la energía no está cuantizada, por lo que puede tomar cualquier valor. A manera de ejemplo, considere \(E=1\) y \(V=10\).

# Valores de m,hbar,E,V

m = 1
hbar = 1
E = 1
V = 10

Defina \(k\) y \(\kappa\), recuerde que

\[ k = \frac{\sqrt{2mE}}{\hbar} \]

\[ \kappa = \frac{\sqrt{2m(V-E)}}{\hbar} \]

# k y kappa

k = np.sqrt(2*m*E)/hbar
kappa = np.sqrt(2*m*(V-E))/hbar

Defina las constantes

\[ B = -\left(\frac{k_2 + ik_1}{k_2 - ik_1}\right) A \]

\[ C = \frac{2ik_1}{ik_1 - k_2} A \]

Por conveniencia, defina

\[ A=1 \]

# A, B, C

A = 1
B = -((kappa + 1j*k)/(kappa - 1j*k))*A
C = 2*1j*k/(1j*k-kappa)*A

Defina el dominio de \(x\) para la región I y para la región II, recuerde que ambos se separan en \(x=0\).

# x1 y x2

x1 = np.linspace(-2,0,100)
x2 = np.linspace(0,2,100)

Genere la eigenfunción para la región I y para la región II. Recuerde

\[ \psi_{\rm I} = A e^{ik x} + B e^{-ik x} \]

\[ \psi_{\rm II} = C e^{-\kappa x} \]

# psi_I y psi_II

psi_I = A*np.exp(1j*k*x1) + B*np.exp(-1j*k*x1)
psi_II = C*np.exp(-kappa*x2)

Grafique \(|\psi_{\rm I}|^2\) y \(|\psi_{\rm II}|^2\)

# Gráfica

plt.plot(x1,abs(psi_I)**2)
plt.plot(x2,abs(psi_II)**2)

[<matplotlib.lines.Line2D at 0x155120daa020>]

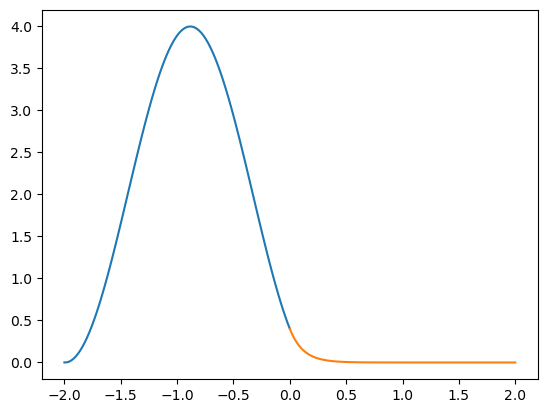
Note que la partícula puede ser encontrada dentro de la región clásicamente prohibida, esto se conoce como penetración.

Concepto: Longitud de decaimiento

La longitud de decaimiento, \(\kappa^{-1}\) es la distancia dentro de la barrera a la cual la eigenfunción ha decaído a \(e^{-1}\).

Calcule la longitud de decaimiento de este sistema.

5.1. Referencias

• P. W. Atkins, y R. Friedman, Molecular Quantum Mechanics (Oxford University Press, 2005).