3. Expansión en series#

Las funciones se pueden representar como una expansión en serie. Una serie es una suma infinita de términos de una sucesión. Representar a una función como una serie es útil para resolver ecuaciones diferenciales o para generar una intución sobre el comportamiento de la función. A continuación se ejemplifica las dos expansiones en serie más usadas: series de Taylor y series de Fourier.

3.1. Serie de Taylor#

Sea una función f(x) continua e infinitamente diferenciable, esta puede expresarse en torno a \(a\) mediante una serie de potencias

\[\begin{equation*} f(x) = \sum_{n=0}^\infty c_n (x-a)^n \end{equation*}\]

donde \(c_n\) es un coeficiente que no depende de \(x\) y que se determinará a continuación.

La m-ésima derivada de \(f(x)\) es:

\[\begin{equation*} f^{(m)}(x) = \sum_{n=m}^\infty c_n\,m!\, (x-a)^{n-m} \>\>. \end{equation*}\]

Realizando el cambio de índice \(p=n-m\) tenemos la expresión:

\[\begin{equation*} f^{(m)}(x) = \sum_{p=0}^\infty c_{p+m}\,m!\, (x-a)^{p} \>\>. \end{equation*}\]

Al evaluar en \(x=a\) se obtiene

\[\begin{equation*} f^{(m)}(a) = \sum_{p=0}^\infty c_{p+m}\,m!\, (a-a)^{p} = c_m\,m! \>\>. \end{equation*}\]

El único término que sobrevive es el que tiene potencia cero, \(p=0\), despejando \(c_m\):

\[\begin{equation*} c_m = \frac{f^{(m)}(a)}{m!} \>\>. \end{equation*}\]

Sustituyendo en la serie

\[\begin{equation*} f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x-a)^n \end{equation*}\]

Aprendizaje de código

A continuación realizaremos la expansión en series de Taylor en torno a \(x=0\) de \(f(x)=e^{x}\) en el intervalo \(x \in [0,10]\) truncada hasta la potencia de grado 6.

Importamos las librerías necesarias

from scipy.misc import derivative
from matplotlib import pyplot as plt
import numpy as np

Definimos la función a aproximar

def f(x):
    return np.exp(x)

Seleccionamos el centro de la expansión en serie

a=0.0

Damos valores a la variable \(x\) en el intervalo establecido en el problema

x=np.linspace(0,10,11)

Sumamos los términos de la serie de Taylor acorde a la ecuación

\[\begin{equation*} f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x-a)^n \end{equation*}\]
y=0
for n in range(0,7):
    y=y+derivative(f,a,n=n,order=2*n+1)/np.math.factorial(n)*(x-a)**n \nonumber

Graficamos la función exacta, \(f(x)\) y la serie de Taylor, \(y\).

plt.scatter(x,y,color='r')
plt.plot(x,f(x))
plt.show()

Haga la expansión en series de Taylor en torno a \(x=0\) de \(f(x)=e^{x}\) en el intervalo \(x \in [0,10]\) truncada hasta la potencia de grado 7 y compárela con la función original.

#Serie de Taylor de f(x)=e^x con x \in [0,10] usando 6 términos
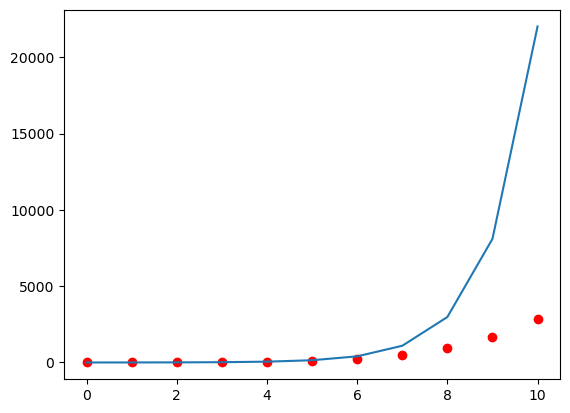
_images/Series_7_0.png

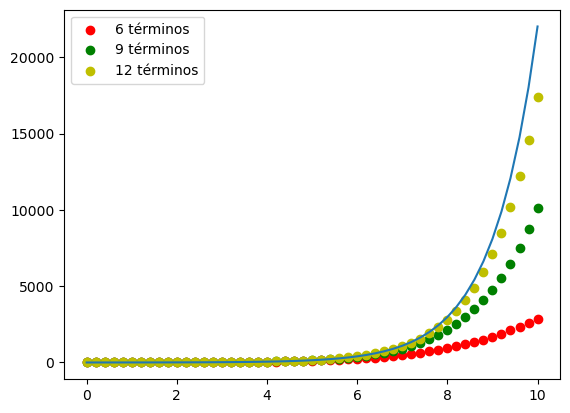
Adapte el código para realizar las series de Taylor de \(f(x)=e^x\) con:

  • 6 Términos

  • 9 Términos

  • 12 Términos

#Series de Taylor de f(x)=e^x con x \in [0,10] usando 6, 9 y 12 términos
_images/Series_10_0.png

Pregunta

¿Qué observa al comparar las series de Taylor truncadas a diferentes grados de potencia con respecto a la función original?

Pregunta

¿Cuál de las expansión en serie de Taylor es más parecida a la función?

La serie truncada hasta la potencia de grado 6.
La serie truncada hasta la potencia de grado 9.
La serie truncada hasta la potencia de grado 12.
Mostrar respuesta
La respuesta correcta es:
La serie truncada hasta la potencia de grado 12.
La serie truncada hasta la potencia de grado 12. Entre más términos se sumen más parecida será la serie truncada a la función, y la igualdad se dará cuando no se trunque ningún término.

3.2. Serie de Fourier#

Una función periódica se puede aproximar por

\[\begin{equation*} f(x)=\frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n \cos \left( \frac{2n\pi}{T}x \right) + b_n \sin \left( \frac{2n\pi}{T}x \right) \right] \end{equation*}\]

donde

\[\begin{equation*} a_0 = \frac{2}{T} \int\limits_{-T/2}^{T/2} f(x) dx \end{equation*}\]
\[\begin{equation*} a_n = \frac{2}{T} \int\limits_{-T/2}^{T/2} f(x) \cos \left( \frac{2n\pi}{T}x \right) dx \end{equation*}\]
\[\begin{equation*} b_n = \frac{2}{T} \int\limits_{-T/2}^{T/2} f(x) \sin \left( \frac{2n\pi}{T}x \right) dx \end{equation*}\]

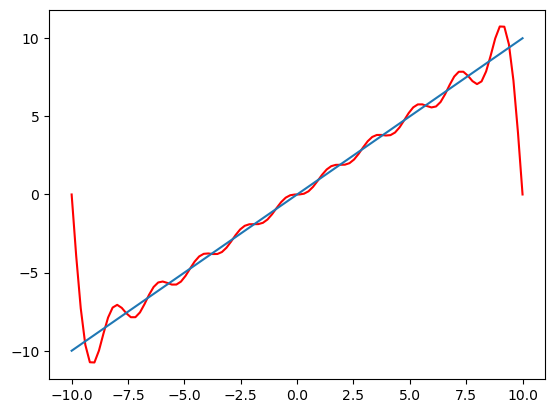
Haga la expansión en series de Fourier de la \(f(x)=x\) en el intervalo \(x \in [-10,10]\) con \(n=10\)

# Serie de Fourier

from scipy import integrate
from matplotlib import pyplot as plt
import numpy as np

a=-10.0
b=10.0

T=b-a

x=np.linspace(a,b,100)

a_0 = 2.0/T*integrate.quad(lambda x: x,a,b)[0]
y = a_0/2.0*x**0.0

for n in range(1,11):
    a_n = 2.0/T*integrate.quad(lambda x: x*np.cos(2*n*np.pi/T*x),a,b)[0]
    b_n = 2.0/T*integrate.quad(lambda x: x*np.sin(2*n*np.pi/T*x),a,b)[0]
    y=y+a_n*np.cos(2*n*np.pi/T*x)+b_n*np.sin(2*n*np.pi/T*x)
    
plt.plot(x,y,color='r')
plt.plot(x,x)
plt.show()
_images/Series_18_0.png

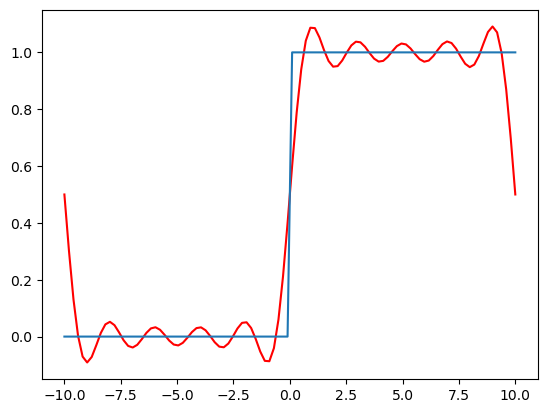
Realice la expansión en series de Fourier de la función escalón en el intervalo \(x \in [-10,10]\) con \(n=10\)

\[\begin{equation*} f(x) = \left\{ \begin{array}{ll} 0 & \mathrm{si\ } x < 0\\ 1 & \mathrm{si\ } x>0 \\ \end{array} \right. \end{equation*}\]
# Serie de Fourier

from scipy import integrate
from matplotlib import pyplot as plt
import numpy as np

a=-10.0
b=10.0

T=b-a

x=np.linspace(-10,10,100)

a_0 = 2.0/T*integrate.quad(lambda x: np.piecewise(x,x>=0,[1,0]),a,b)[0]
y = a_0/2.0*x**0.0

for n in range(1,11):
    a_n = 2.0/T*integrate.quad(lambda x: np.piecewise(x,x>=0,[1,0])*np.cos(2*n*np.pi/T*x),a,b)[0]
    b_n = 2.0/T*integrate.quad(lambda x: np.piecewise(x,x>=0,[1,0])*np.sin(2*n*np.pi/T*x),a,b)[0]
    y=y+a_n*np.cos(2*n*np.pi/T*x)+b_n*np.sin(2*n*np.pi/T*x)
    
plt.plot(x,y,color='r')
plt.plot(x,np.piecewise(x,x>=0,[1,0]))
plt.show()
_images/Series_21_0.png

3.3. Referencias#

  • G.P. Tolstov, Fourier Series (Dover ed., 1992).

  • J.D. Jackson, Mathematics for Quantum Mechanics: An Introductory Survey of Operators, Eigenvalues, and Linear Vector Spaces (Dover ed., 2006).

  • J.L. Gersting, Technical Calculus with Analytic Geometry (Dover ed., 2009).