15. Teoría de perturbaciones (niveles de energía no degenerados)#

El objetivo es determinar una solución aproximada a la ecuación de Schrödinger para un Hamiltoniano \(\hat{H}\). La suposición importante en la teoría de perturbaciones es que \(\hat{H}\) es un poco diferente de un Hamiltoniano \(\hat{H}^{(0)}\) del cual conocemos su solución; es decir, conocemos sus eigenfunciones y eigenvalores. Esto es

\[ \hat{H}^{(0)} \psi_n^{(0)} = E_n^{(0)} \psi_n^{(0)} \]

donde tanto \(E_n^{(0)}\) y \(\psi_n^{(0)}\) son conocidos. La diferencia entre \(\hat{H}\) y \(\hat{H}^{(0)}\) se llama la perturbación y la denotamos por \(\hat{H}'\), esto es

\[ \hat{H}' = \hat{H}-\hat{H}^{(0)} \]

El método presentado en este notebook tiene la suposición los niveles de energía \(\big\{ E_n^{(0)}\big\}\) no están degenerados.

Proponemos una solución en serie aproximada a los eigenvalores (\(E_n\)) y las eigenfunciones (\(\psi_n\)) de \(\hat{H}\) en términos de \(E_n^{(0)}\) y \(\psi_n^{(0)}\) y correcciones a dichos valores. De tal forma que tenemos,

\[\begin{split} E_n &=& E_n^{(0)}+ E_n^{(1)} + E_n^{(2)} +\ldots \\ \psi_n &=& \psi_n^{(0)}+\psi^{(1)}+\psi^{(2)}+\ldots \end{split}\]

Inserto matemático: Correcciones

Con el fin de escribir las expresiones para las diferentes correcciones introducimos la notación para los elementos de matriz de la perturbación, (\(\hat{H}'\)),

\[ \hat{H}'_{m,n} = \langle \psi_m^{(0)} | \hat{H}' | \psi_n^{(0)} \rangle = \int \big( \psi_m^{(0)} \big)^* \hat{H}' \psi_n ^{(0)} \,dq \]

donde \(\psi_n^{(0)}(q)\) son la eigenfunciones que conocemos de \(\hat{H}^{(0)}\) y hemos denoatdo por \(q\) a las coordenadas de las que dependen.

En términos de los elementos de matriz de \(\hat{H}'\) tenemos,

\[ E_n \approx E_n^{(0)} +H'_{n,n} + \sum_{m \neq n } \frac{|H'_{m,n}|^2}{E_n^{(0)}-E_m^{(0)}} \]

y

\[ \psi_n \approx \psi_n^{(0)} + \sum_{m\neq n} \frac{\hat{H}'_{m,n}}{E_n^{(0)}-E_m^{(0)}} \psi_m^{(0)} \]

15.1. Ejemplo - Oscilador anarmónico#

En Hamiltoniano del oscilador anarmónico de una partícula en una dimensión es:

\[ \hat{H} = \underbrace{-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2} k x^2 }_{\hat{H}^{(0)}} + \underbrace{cx^3 + dx^4}_{\hat{H}'} \]

Los eigenvalores y eigenfunciones del oscilador armónico son:

\[ E_n^{(0)} = \bigg(n+\frac{1}{2}\bigg) h\nu \]
\[ \psi_n^{(0)} (x) = \frac{1}{\sqrt{2^n n !}} \bigg( \frac{\alpha}{\pi} \bigg)^{1/4} e^{-\alpha x^2/2 } H_n\bigg( \alpha^{1/2}\,x \bigg) \]

donde \(\alpha = 2\pi\nu m /\hbar\) y

\[ \nu = \frac{1}{2\pi }\bigg( \frac{k}{m} \bigg)^{1/2} \]

Realicemos numéricamente el cálculo de los elementos de matriz.

Importe las siguientes librerías

  • pylab

  • scipy.special

De la librería scipy.special ocuparemos las funciones factorial y eval_hermite

# Librerías

from pylab import *
from scipy.special import factorial
from scipy.special import eval_hermite as Hn

Defina los valores de los parámetros y constantes a usar.

Tomemos de ejemplo los valores de la molécula de CO.

Parámetro

Valor

\(k\)

\(1902.5\,{\rm N/m}\)

\(\mu\)

\(1.1391 \times10^{-26}\,{\rm kg}\)

\(\nu\)

\(\displaystyle \frac{1}{2\pi}\sqrt{\frac{k}{m}}\)

\(\alpha\)

\(2\pi\nu m/\hbar \)

 
# Defina los valores y constantes en el Hamiltoniano del oscilador armónico 
# e imprima los valores de ν y el valor del E = hν/2

π = pi
k = 1902.5             # [ N·m^{-1}]  constante de fuerza del CO
m = 1.1391e-26         # [kg] masa reducida de C-O
ħ = 1.0545718e-34      # [J·s] 
h = 2*pi*ħ
e = 1.602e-19
ν = 0.5*sqrt( k/m )/π
α = 2*π*ν*m/ħ          # [m^{-2}]

print ("    ν  = {0:.3e} [Hz]".format(ν))
print ("√(1/α) = {0:.3e} [m]".format(1/sqrt(α)))

# n -> nivel de energía
n   = 0

# Definimos una función que nos dé la eigenenergía del 
# oscilado armónico
def eigenEn0(n):
    return (n+0.5) *h*ν

E00 = eigenEn0(0)

print ("E0^(0) = {0:.3f} [eV]".format(E00/e))
# Notemos que al imprimir el valor de E00 dividimos
# por la carga elemental para obtener las unidades de eV.

    ν  = 6.504e+13 [Hz]
√(1/α) = 4.760e-12 [m]
E0^(0) = 0.135 [eV]

Defina las eigenfunciones del oscilador armónico.

# Define como función de python las eigenfunciones del oscilador armónico

# Definimos la función que nos devuelva la eigenfunción 
# del oscilador armónico
def funcΨ0n(n,x):
    return ( 1/sqrt(2**n*factorial(n)) )*( (α/π)**(0.25) )*exp(-α*x*x/2)*Hn(n,sqrt(α)*x)

Verifica la normalización de las eigenfunciones

# Define un intervalo donde evaluar la función y la integral
# La integral numérica de una función puede realizarse con 
# la función numpy.trapz

# La longitud (1/α)^{1/2} es característica de las eigenfunciones 
# por lo que es un buen parámetro para determinar el intervalo de 
# los valores de x.

x   = linspace(-10/sqrt(α),10/sqrt(α),10000)
Ψ0n = funcΨ0n(n,x)

# Podemos verificar que las eigenfunciones están normalizadas utilizando la regla del trapecio
# Notemos que las eigenfunciones son reales por lo que Ψ*(x) = Ψ(x)
Ψ2       = Ψ0n*Ψ0n
Integral = trapz(Ψ2,x)
print ("Integral: {0:.3f}".format(Integral))

Integral: 1.000

Evalúa los elementos de matriz de \(H'=cx^3+dx^4\)

Utiliza que \(c=600\,{\rm J}/{\rm m}^3\) y \(d=1\times 10^{-4}\alpha k^2/4\)

# Define H' y define una función para evaluar 
# los elementos de matriz dado un m y n

# Definimos la perturbación H'
c  = 600; d = 1e-4*(α*k*k)/4

Hp = c*x**3 + d*x**4

# Definimos la función que evalúa
def ElementoMatriz(m,n,x):
    Ψm0 = funcΨ0n(m,x)
    Ψn0 = funcΨ0n(n,x)
    Int = trapz( Ψm0*Hp*Ψn0,x )
    return Int

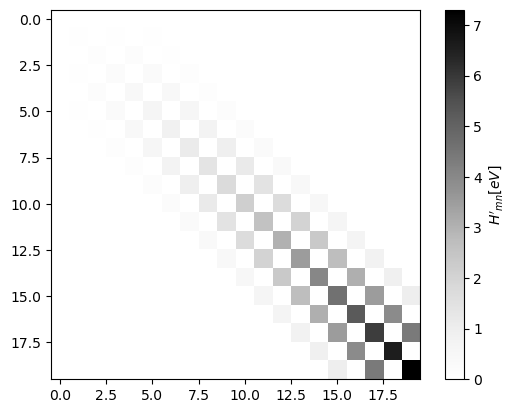
Visualiza los elementos de matriz

# Construimos los elementos de matriz de H'_{m,n}
# Notemos que numéricamente la matriz
# tiene un tamaño finito
m_max = 20

matrizHp = zeros((m_max,m_max))

for m in range(m_max):
    for n in range(m_max):
        matrizHp[(m,n)] = ElementoMatriz(m,n,x)

# Las matrices se pueden visualizar utilizando un mapa de colores
plotM = imshow(matrizHp/e,cmap="Greys");
plt.colorbar(label="$H'_{mn} [eV]$");
# Notamos como los valores distinto de cero están cerca de la diagonal
# lo cual es típico en la teoría de perturbaciones
_images/PerturbacionesSinDegeneracion_19_0.png

15.1.1. Corrección a primer orden (analítico vs numérico)#

La corrección a primer orden de la energía de la energía del estado base es,

\[ E_0^{(1)} = \frac{3d}{4\alpha^2} = \frac{3dh^2}{64\pi^4 \nu^2 m^2} \]

¿Podría verificarla numéricamente?

# Compare la expresión analítica con la corrección a primer orden

# Solución

# De acuerdo con la expresión analítica
E01analitico = 3*d/4/α/α
print ("E0^(1) = {0:.3e} [eV]".format(E01analitico/e))

# De la teoría de perturbaciones tenemos que
# E0^(1) = H'_{0,0}
E01numerico = matrizHp[(0,0)]
print ("E0^(1) = {0:.3e} [eV]".format(E01numerico/e))

E00 = eigenEn0(0)

print ("E0^(0) = {0:.3e} [eV]".format(E00/e))

# Por tanto la aproximación a primer orden en la energía es:
print ("    En ≈ {0:.3e} [eV]".format(E00/e + E01numerico/e))
# ¿La energía es mayor o menor a la del oscilador armónico?

E0^(1) = 9.597e-03 [eV]
E0^(1) = 9.597e-03 [eV]
E0^(0) = 1.345e-01 [eV]
    En ≈ 1.441e-01 [eV]

15.1.2. Correcciones a primer orden (niveles excitados)#

¿Podría calcular la corrección a primer orden del primer nivel excitado del oscilador armónico?

# Calcule las correcciones a primer orden de n>0

# Solución

# De la teoría de perturbaciones tenemos que
# E1^(1) = H'_{1,1}
E11numerico = matrizHp[(1,1)]
print ("E1^(1) = {0:.3e} [eV]".format(E11numerico/e))

E10 = eigenEn0(1)

print ("E1^(0) = {0:.3e} [eV]".format(E10/e))

# Por tanto la aproximación a primer orden en la energía es:
print ("    En ≈ {0:.3e} [eV]".format(E10/e + E11numerico/e))
# ¿La energía es mayor o menor a la del oscilador armónico?

E1^(1) = 4.798e-02 [eV]
E1^(0) = 4.035e-01 [eV]
    En ≈ 4.515e-01 [eV]

15.1.3. Correcciones a primer orden (primeros 5 niveles)#

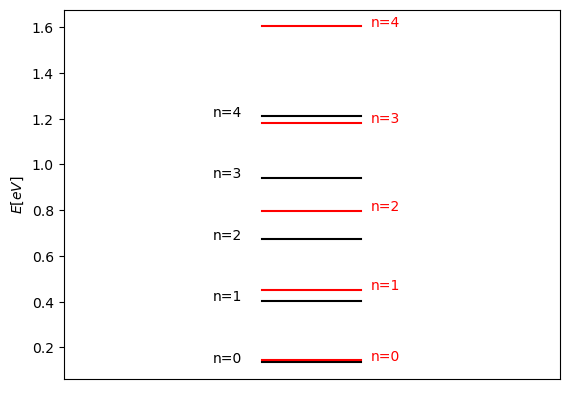
Realiza un gráfico de los primeros 5 niveles de energía del oscilador armónico y los niveles con la primera corrección a la energía.

# Solución

En1numerico = array( [ matrizHp[n,n] for n in range(5) ] )

En0         = array( [ eigenEn0(n) for n in range(5) ] )

Enapprox    = En0 + En1numerico

for n in range(5):
    plot( [0,1],[En0[n]/e,En0[n]/e],c='k' )
    plot( [0,1],[Enapprox[n]/e,Enapprox[n]/e],c='r' )
    text(-0.5,En0[n]/e,"n={0}".format(n))
    text( 1.1,Enapprox[n]/e,"n={0}".format(n),color='r')
xlim(-2,3)
xticks([])
ylabel("$E [eV]$")

Text(0, 0.5, '$E [eV]$')
_images/PerturbacionesSinDegeneracion_29_1.png

15.1.4. Corrección a segundo orden#

De la teoría de perturbaciones tenemos que

\[ E_n ^{(2)}=\sum_{m \neq n } \frac{|H'_{m,n}|^2}{E_n^{(0)}-E_m^{(0)}} \]
# Previamente realizamos el gráfico de los elementos de matriz

# Las matrices se pueden visualizar utilizando un mapa de colores
plotM = imshow(matrizHp/e,cmap="Greys");
plt.colorbar(label="$H'_{mn} [eV]$");
# Notamos como los valores distinto de cero están cerca de la diagonal
# lo cual es típico en la teoría de perturbaciones
_images/PerturbacionesSinDegeneracion_31_0.png 
# Sin embargo, los términos a sumar son los elementos de matriz 
# al cuadrado divididos por la diferencia de energía del nivel a corregir.

# Analicemos los términos de la suma cuando n = 0, es decir el estado base
n   = 0
E00 = eigenEn0(0) 
# Dado que las eigenfunciones son reales no tenemos que tomar el conjugado
SegundoOrden = array( [ matrizHp[(m,n)]*matrizHp[(m,n)]/( eigenEn0(n)-eigenEn0(m) ) \
                    for m in range(m_max) if m != n ] )

# Grafiquemos los SegundoOrden
plot(range(1,m_max),SegundoOrden/e,'o-');
xticks([1,2,3,4,5,6,7]);
ylabel("$E$ [eV]")
xlabel("m");

#Podemos notar en este caso que la mayor corrección al estado base proviene del nivel n = 2
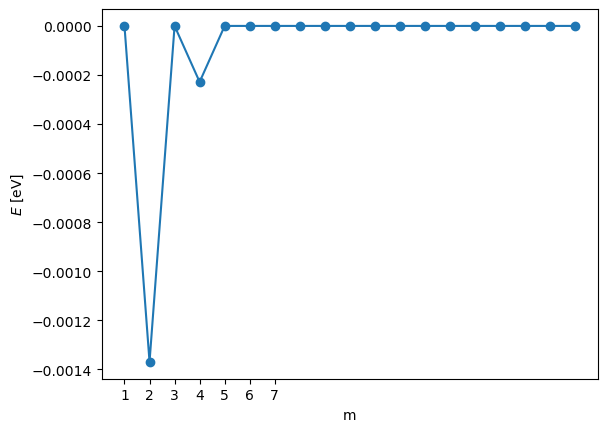
_images/PerturbacionesSinDegeneracion_33_0.png 
# Notamos que los sumandos siempre son negativos para el estado base
print (" Máximo valor de los sumandos: {0:.3e} eV".format( max(SegundoOrden)/e ))
# Por lo que las correcciones de segundo orden disminuirán con respecto a 
# las de primer orden.

 Máximo valor de los sumandos: -3.143e-41 eV

15.1.5. Correcciones primer orden vs segundo orden#

Realiza un gráfico de los primeros 5 niveles de energía del oscilador armónico y los niveles con la segunda corrección a la energía. ¿Es muy diferente al resultado de la corrección a primer orden?

# Solución

def SumaSegundoOrden(n,m_max=20):
    SegundoOrden = array( [ matrizHp[(m,n)]*matrizHp[(m,n)]/( eigenEn0(n)-eigenEn0(m) ) \
                        for m in range(m_max) if m != n ] )
    En2 = SegundoOrden.sum()
    return En2


En1numerico = array( [ matrizHp[n,n] for n in range(5) ] )

En2numerico = array( [ SumaSegundoOrden(n) for n in range(5) ] )

En0         = array( [ eigenEn0(n) for n in range(5) ] )


Enapprox1 = En0 + En1numerico
Enapprox2 = En0 + En1numerico + En2numerico


plot( [0,1],[En0[0]/e,En0[0]/e],c='k',label='(0)' )
plot( [0,1],[Enapprox1[0]/e,Enapprox1[0]/e],c='r',label='1er' )
plot( [0,1],[Enapprox2[0]/e,Enapprox2[0]/e],c='b',label='2d0' )
text(-0.5,En0[0]/e,"n={0}".format(n))
text( 1.1,Enapprox1[0]/e,"n={0}".format(n),color='r')
text( 1.5,Enapprox2[0]/e,"n={0}".format(n),color='b')
for n in range(1,5):
    plot( [0,1],[En0[n]/e,En0[n]/e],c='k' )
    plot( [0,1],[Enapprox1[n]/e,Enapprox1[n]/e],c='r' )
    plot( [0,1],[Enapprox2[n]/e,Enapprox2[n]/e],c='b' )
    text(-0.5,En0[n]/e,"n={0}".format(n))
    text( 1.1,Enapprox1[n]/e,"n={0}".format(n),color='r')
    text( 1.5,Enapprox2[n]/e,"n={0}".format(n),color='b')
xlim(-1,3)
xticks([])
ylabel("$E [eV]$");
legend(loc=0);
_images/PerturbacionesSinDegeneracion_37_0.png