4. Partícula en la caja#

A continuación estudiaremos sistemas sencillos que nos permiten entender como surge la cuantización. Además, nos permitirán familiarizarnos con los pasos para resolver los problemas de química cuántica. Podemos resumir estos como:

Identificar las interacciones y restricciones del sistema.
Escribir el Hamiltoniano (\(\mathcal{H}\)) y la ecuación de Schrödinger (\(\mathcal{H}\psi = E \psi\)).
Determinar las eigenfunciones (\(\psi\)).
Estudiar las condiciones de cuantización.

4.1. Caja 1D#

La versión 1D de este sistema consiste en una partícula que se mueve en el espacio con un potencial definido en tres regiones

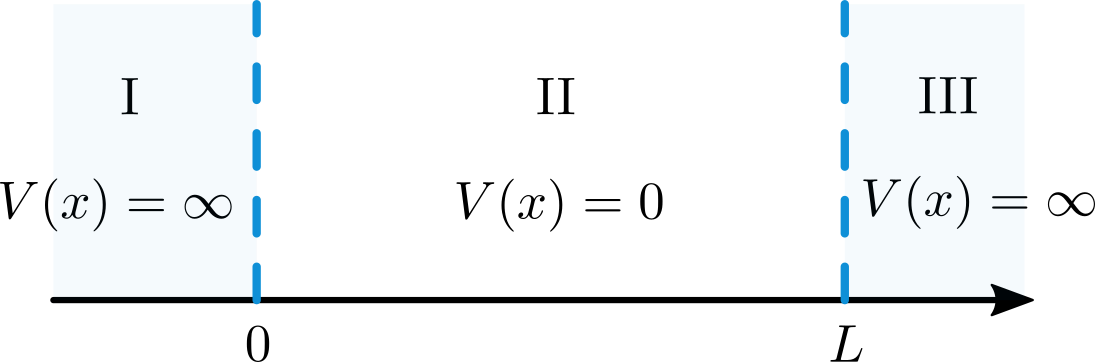
es decir

\[\begin{split} V(x) = \left\{ \begin{array}{lll} \infty & \mathrm{si\ } x < 0 & \text{I}\\ 0 & \mathrm{si\ } 0 \le x \le L & \text{II} \\ \infty & \mathrm{si\ } x > L & \text{III} \end{array} \right. \end{split}\]

Esto significa que la partícula está confinada a un intervalo en \(x \in [0,L]\).

La eigenfunción se puede dividir por regiones. Es imposible que la partícula se encuentre en la región \({\rm I}\) y en la región \({\rm III}\), ya que el potencial es infinito, por lo tanto:

\[\begin{split} \psi(x) = 0 \left\{ \begin{array}{lll} \mathrm{si\ } x < 0 & \text{I}\\ \mathrm{si\ } x > L & \text{III} \end{array} \right. \end{split}\]

Para determinar la eigenfunción en la región \(\text{II}\) hay que escribir la ecuación de Schrödinger

\[\begin{equation*} \left(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \right)\psi(x) = E \psi(x) \end{equation*}\]

cuya solución es

\[\begin{equation*} \psi(x) = A\cos(kx) + B\sin(kx) \>\>\>\>\> \mathrm{si\ } 0 \leq x \leq L; \>\>\>\>\> k^2 = \frac{2mE}{\hbar^2} \end{equation*}\]

posteriormente hay que recurrir a las condiciones a la frontera.

Inserto matemático: Condiciones a la frontera

La eigenfunción debe ser continua, esto significa que la región I y la región II deben unirse en el mismo punto, es decir, \(\psi_{\rm I}(0) = \psi_{\rm II}(0) = 0\). Esto implica que \(A=0\), ya que

\[\begin{equation*} \psi_{\rm II}(0) = 0 = A\cos(0) + B\sin(0) = A \end{equation*}\]

Por la continuidad con la región III también se cumple \(\psi_{\rm II}(L) = \psi_{\rm III}(L) = 0\), es decir

\[\begin{equation*} \psi_{\rm II}(L) = 0 = B\sin(kL) \end{equation*}\]

Ya obtuvimos que \(A\) vale cero, sin embargo, \(B\) no puede ser cero porque \(\psi_{\rm II}\) se anularía. La única forma de que se cumpla la condición a la frontera expresada en la ecuación anterior es que \(kL\) sea un múltiplo de \(\pi\), es decir \(kL = n \pi\), o lo que es lo mismo

\[\begin{equation*} k=\frac{n\pi}{L};\>\>\>\>\> n=1,2,3,\cdots \end{equation*}\]

Note que en este punto, \(k\), y por tanto la energía, ya no pueden tomar cualquier valor, ¡se han cuantizado!.

Hemos obtenido que

\[\begin{equation*} \psi_{\rm II} = B \sin \left( \frac{n \pi x}{L}\right) \end{equation*}\]

Para determinar el valor de B hay que normalizar la eigenfunción, resultando que en la región \({\rm II}\):

\[\begin{equation*} \psi_n(x)=\left(\frac{2}{L}\right)^{1/2}\sin\left(\frac{n\pi x}{L}\right) \end{equation*}\]

Finalmente, la energía toma la forma

\[\begin{equation*} E = \frac{\hbar^2 k^2}{2m} = \frac{h^2 n^2}{8mL^2} = \frac{\hbar^2 \pi^2 n^2}{2mL^2}; \>\>\>\>\> n=1,2,3,\cdots \end{equation*}\]

Estado base y estados excitados

El estado base del sistema se define como el estado de mínima energía, mientras que los estados de mayor energía se denominan estados excitados. El estado base de la partícula en la caja corresponde a \(n = 1\), y los estados excitados corresponden a \(n = 2,3,\cdots\).

Importe las siguientes librerías

numpy
pyplot de matplotlib

#librerias

import numpy as np
from matplotlib import pyplot as plt

Considere un electrón dentro de una caja de longitud 4 Angstroms. Defina las siguientes constantes

hbar = 1
m = 1
L = 4

# Constantes

hbar = 1
m = 1
L = 4

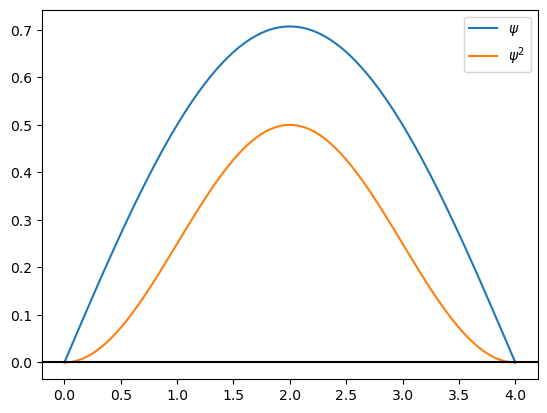
Grafique la eigenfunción (\(\psi\)) y su cuadrado (\(\psi^2\)) para n=1 y L=4.0 A

Tip

Declare la variable n asígnele su valor.
Cree el dominio de x de 0 a L con numpy.linspace, utilice una cantidad de puntos, por ejemplo 100.
Evalúe la eigenfunción en el dominio
Calcule el cuadrado de la eigenfunción en el dominio
Grafique la eigenfunción y su cuadrado usando matplotlib y pyplot.

# Inserte código para gráfica

# Gráfica de psi_1 y su cuadrado

n=1

x=np.linspace(0,L,100)

psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
psi2=psi*psi

plt.plot(x,psi,label="$\psi$")
plt.plot(x,psi2,label="$\psi^2$")

plt.legend()
plt.axhline(y=0, color='k')
plt.show()

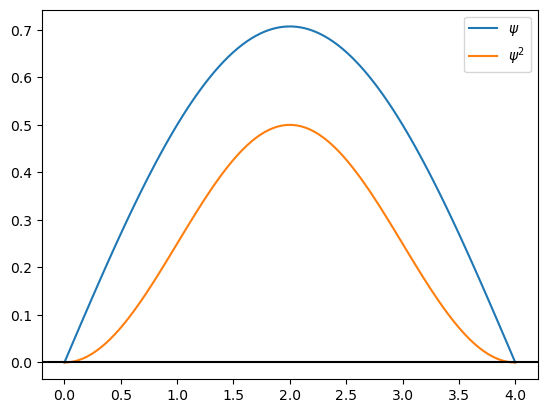
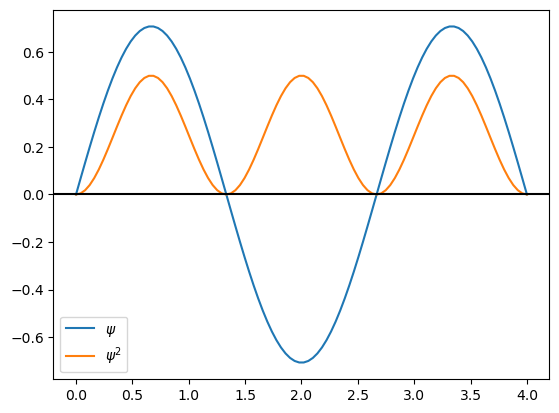
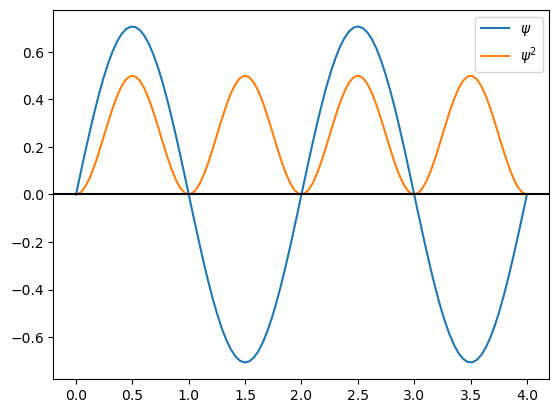
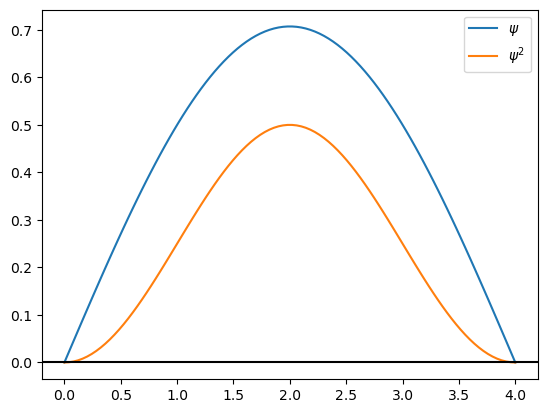
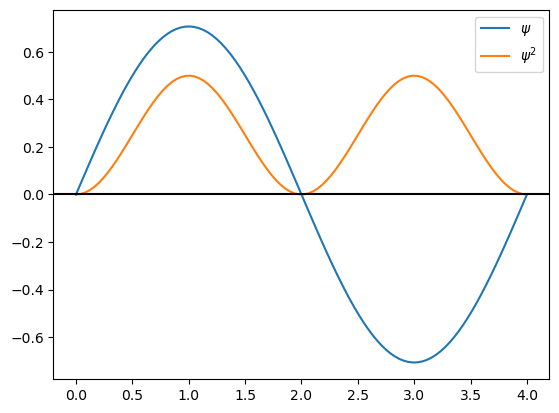
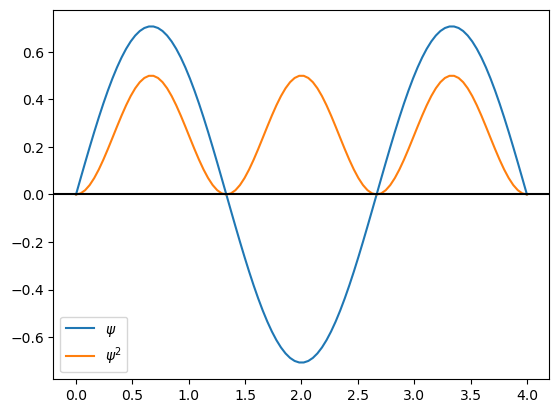
Grafique la eigenfunción (\(\psi\)) y su cuadrado (\(\psi^2\)) para n=1,2,3,4 para L=4.0 A

Tip

Cree el dominio de x de 0 a L con numpy.linspace, utilice una cantidad de puntos, por ejemplo 100.
Evalúe las 4 eigenfunciones en el dominio.
Calcule el cuadrado de las 4 eigenfunciones en el dominio.
Grafique las funciones y su cuadrado usando matplotlib y pyplot.

# Inserte código para gráfica

# Gráfica de psi_1, psi_2, psi_3, psi_4 y su cuadrado

x=np.linspace(0,L,100)

n=1

psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
psi2=psi*psi
plt.plot(x,psi,label="$\psi$")
plt.plot(x,psi2,label="$\psi^2$")

plt.legend()
plt.axhline(y=0, color='k')
plt.show()

n=2

psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
psi2=psi*psi
plt.plot(x,psi,label="$\psi$")
plt.plot(x,psi2,label="$\psi^2$")

plt.legend()
plt.axhline(y=0, color='k')
plt.show()

n=3

psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
psi2=psi*psi
plt.plot(x,psi,label="$\psi$")
plt.plot(x,psi2,label="$\psi^2$")

plt.legend()
plt.axhline(y=0, color='k')
plt.show()

n=4

psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
psi2=psi*psi
plt.plot(x,psi,label="$\psi$")
plt.plot(x,psi2,label="$\psi^2$")

plt.legend()
plt.axhline(y=0, color='k')
plt.show()

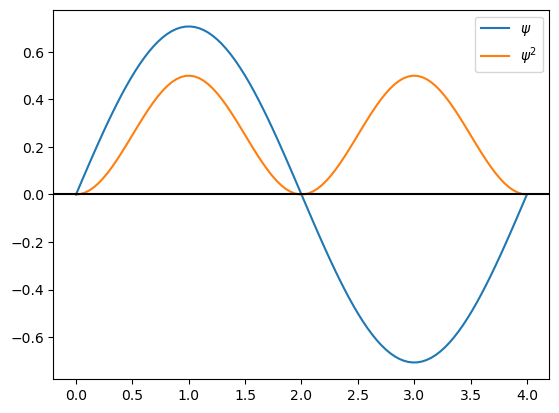
Pregunta

Encuentre un patrón entre el número cuántico \(n\), el número de nodos de la eigenfunción, y el número de máximos del cuadrado de la eigenfunción.

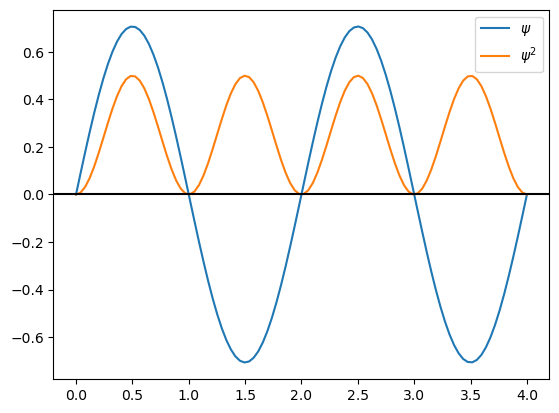
Como estamos haciendo una secuencia de gráficas donde aumentamos n de uno en uno, podemos hacerlo con un ciclo for. Repita la gráfica de las eigenfunciones con \(n=1,2,3,4\) utilizando un ciclo for.

# Inserte código para 4 gráficas en las que solo cambia el valor de n, use un for

# Gráfica de psi_1, psi_2, psi_3, psi_4 y su cuadrado con for

x=np.linspace(0,L,100)

for n in range(1,5):
    psi=np.sqrt(2.0/L)*np.sin(n*np.pi*x/L)
    psi2=psi*psi
    plt.plot(x,psi,label="$\psi$")
    plt.plot(x,psi2,label="$\psi^2$")
    plt.legend()
    plt.axhline(y=0, color='k')
    plt.show()

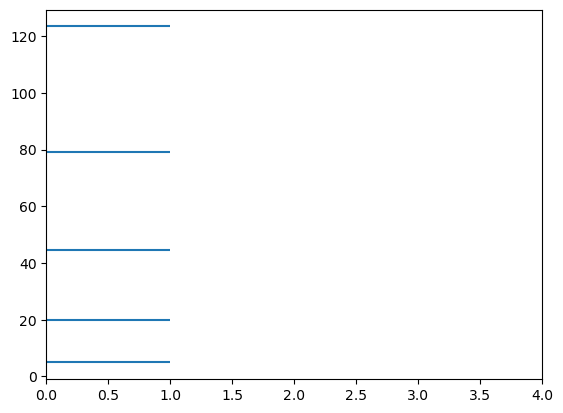
Haga la gráfica de E en función de n para los primeros 5 niveles energéticos de un electrón en una caja.

Tip

\[\begin{equation*} E = \frac{\hbar^2 \pi^2 n^2}{2mL^2} \end{equation*}\]

Con \(n=1,2,3\cdots\)

Utilice la instrucción

plt.hlines(valor,inicio,fin)

Para trazar líneas horizontales desde inicio hasta fin del eje X en valor del eje Y.

Alternativamente, también puede graficar \(n\) vs \(E\bigg/\frac{\hbar^2 \pi^2}{2mL^2}\)

# Inserte código para gráfica

L = 1

for n in range(1,6):
    plt.hlines(hbar**2*np.pi**2*n**2/(2*m*L**2),0,1)

plt.xlim(0,4)
plt.show()

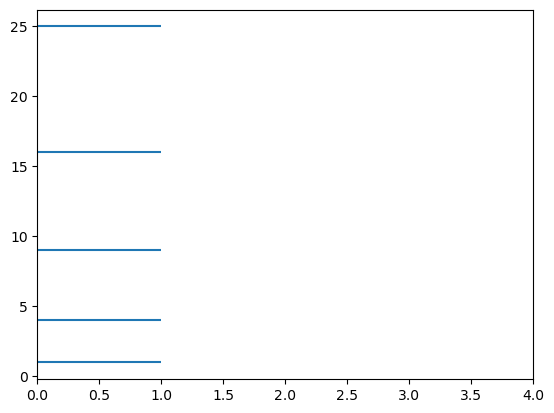
L = 1

for n in range(1,6):
    plt.hlines(n**2,0,1)

plt.xlim(0,4)
plt.show()

Pregunta

¿Qué causó la cuantización de la energía de la partícula en la caja?

Muestre que \(\psi_1\) y \(\psi_3\) son ortonormales (Tome \(L=2.0\)).

Tip

Haga las integrales

\[ \int_0^L \psi_1 \psi_1 dx = 1 \]

\[ \int_0^L \psi_3 \psi_3 dx = 1 \]

\[ \int_0^L \psi_1 \psi_3 dx = 0 \]

# Integral

import numpy as np
from scipy import integrate

L=2.0

psi_1psi_1 = integrate.quad(lambda x: np.sqrt(2.0/L)*np.sin(np.pi*1.0*x/L)*np.sqrt(2.0/L)*np.sin(np.pi*1.0*x/L),0,L)[0]
psi_3psi_3 = integrate.quad(lambda x: np.sqrt(2.0/L)*np.sin(np.pi*3.0*x/L)*np.sqrt(2.0/L)*np.sin(np.pi*3.0*x/L),0,L)[0]

psi_1psi_3 = integrate.quad(lambda x: np.sqrt(2.0/L)*np.sin(np.pi*1.0*x/L)*np.sqrt(2.0/L)*np.sin(np.pi*3.0*x/L),0,L)[0]

print("Integrales")
print("psi_1psi_1",psi_1psi_1)
print("psi_3psi_3",psi_3psi_3)
print("psi_1psi_3",psi_1psi_3)

Integrales
psi_1psi_1 1.0
psi_3psi_3 1.0000000000000002
psi_1psi_3 4.163336342344337e-17

Pregunta

La energía del estado base de una partícula en una caja es cero.

Mostrar respuesta

La respuesta correcta es:
Falso
Dado que si \(E=0\) entonces \(\psi =0\) y dicha solución no cumple que su cuadrado sea una densidad de probabilidad.

4.2. Caja 2D#

El problema se puede plantear como una partícula en una caja de 2-Dimensiones. En este caso, la partícula se confina en \(x \in [0,L_x]\) y \(y \in [0,L_y]\).

La ecuación de Schrödinger a resolver es

\[\begin{equation*} -\frac{\hbar^2}{2m} \left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right)\psi(x,y)=E\psi(x,y) \end{equation*}\]

Que se resuelve por el método de separación de variables y se obtiene:

\[\begin{equation*} k_x=\frac{n_x\pi}{L_x}; \>\>\>\>\> n_x=1,2,3,\cdots \end{equation*}\]

\[\begin{equation*} k_y=\frac{n_y\pi}{L_y}; \>\>\>\>\> n_y=1,2,3,\cdots \end{equation*}\]

\[\begin{equation*} \psi_{n_x,n_y}(x,y)=\left(\frac{2}{L_x}\right)^{1/2} \left(\frac{2}{L_y}\right)^{1/2}\sin\left(\frac{n_x\pi x}{L_x}\right)\sin\left(\frac{n_y\pi y}{L_y}\right) \end{equation*}\]

\[\begin{equation*} E = \frac{h^2 }{8m} \left(\frac{n_x^2}{L_x^2} + \frac{n_y^2}{L_y^2} \right) \end{equation*}\]

A continuación realizará una serie de pasos que le permitirán generar la gráfica de \(\psi_{1,1}\), es decir \(n_x=1\) y \(n_y=1\), y de \(|\psi_{1,1}|^2\) con \(L_x = L_y = 4.0\)

Para hacer gráficas 3D, declararemos el siguiente código

ax = plt.axes(projection='3d')

# Ejes 3D

ax = plt.axes(projection='3d')

Declare los valores de Lx=4, Ly=4, nx=1 y ny=1

#valores

Lx=4.0
Ly=4.0

nx=1.0
ny=1.0

Es muy frecuente que las gráficas de superficies requieran de un mallado.

Tip

Genere un mallado con las siguientes instrucciones

1 Declare un dominio para sus ejes, en este caso \(x\in[0,L_x]\) y \(y\in[0,L_y]\)

x = np.linspace(0, Lx, 30x = np.linspace(0, Lx, 30)
y = np.linspace(0, Ly, 30)

2 Genere el mallado con la instrucción meshgrid

X, Y = np.meshgrid(x, y)

# Mallado

x = np.linspace(0, Lx, 30)
y = np.linspace(0, Ly, 30)
X, Y = np.meshgrid(x, y)

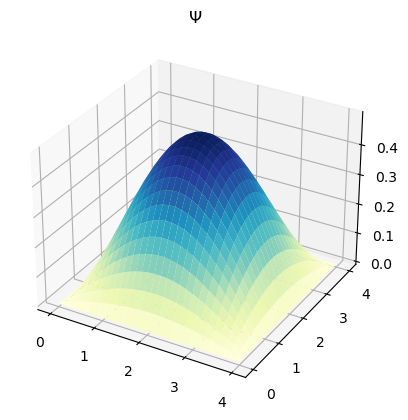
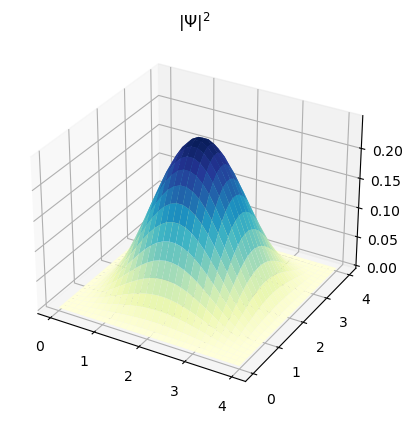
Genere la gráfica de \(\psi_{1,1}\), es decir \(n_x=1\) y \(n_y=1\), y de \(|\psi_{1,1}|^2\) con \(L_x = L_y = 4.0\).

Tip

Use el siguiente código. Note el uso de plt.axes para crear un eje 3D, y de ax.plot_surface

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$\Psi$")
plt.show()

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi**2.0, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$|\Psi|^2$")
plt.show()

# Inserte código para gráfica

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$\Psi$")
plt.show()

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi**2.0, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$|\Psi|^2$")
plt.show()

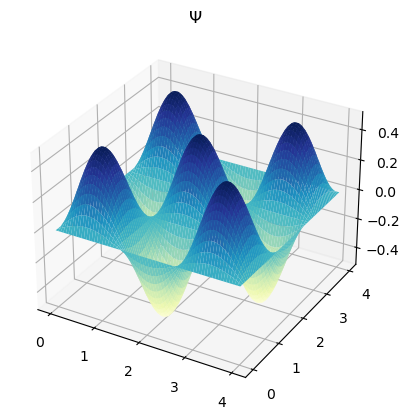
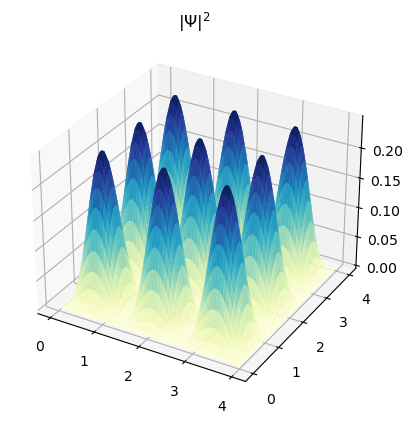
Obtenga la gráfica de \(\psi_{3,3}\) y \(|\psi_{3,3}|^2\) con \(L_x = L_y = 4.0\)

Tip

Declare los valores de \(L_x\), \(L_y\), \(n_x\) y \(n_y\).
Genere el mallado
Genere la gráfica de \(\psi\) y \(\psi^2\).

# Inserte código para gráfica

Lx=4.0
Ly=4.0

nx=3.0
ny=3.0

x = np.linspace(0, Lx, 70)
y = np.linspace(0, Ly, 70)
X, Y = np.meshgrid(x, y)

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$\Psi$")
plt.show()

psi = np.sqrt(2.0/Lx)*np.sqrt(2.0/Ly)*np.sin(nx*np.pi*X/Lx)*np.sin(ny*np.pi*Y/Ly)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, psi**2.0, rstride=1, cstride=1,
                cmap='YlGnBu', edgecolor='none')
ax.set_title("$|\Psi|^2$")
plt.show()

4.3. Referencias#

G.L. Breneman, The Two-Dimensional Particle in a Box, J. Chem. Educ. 67, 866 (1990).
P.L. Lang y M.H. Towns, Visualization of Wavefunctions using Mathematica, J. Chem. Educ. 75, 506 (1998).
T. Kippeny, L.A. Swafford, y S.J. Rosenthal, Semiconductor Nanocrystals: A Powerful Visual Aid for Introducing the Particle in a Box, J. Chem. Educ. 79, 1094 (2002).
B.D. Anderson, Alternative Compounds for the Particle in a Box Experiment, J. Chem. Educ. 74, 985 (1997).
F.L. Pilar, Elementary Quantum Chemistry (Dover ed., 2001).

Cuántica I

Partícula en la caja

Contents

4. Partícula en la caja#

4.1. Caja 1D#

4.2. Caja 2D#

4.3. Referencias#