7. Partícula en el anillo#

Es el sistema de una partícula moviéndose en una trayectoria de radio constante tal que \(x^2 + y^2 = r^2\).

Inserto matemático: Hamiltoniano del sistema

El Hamiltoniano para una partícula en dos dimensiones, tanto en coordenadas cartesianas como en coordenadas polares es

\[ H = -\frac{\hbar^2}{2m} \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right) = -\frac{\hbar^2}{2mr^2} \left( \frac{\partial^2}{\partial r^2} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{1}{r^2} \frac{\partial^2}{\partial \phi^2} \right) \]

Como \(r\) es constante en el anillo, entonces se eliminan las derivadas respecto a \(r\), y el Hamiltoniano se vuelve más simple

\[ H = -\frac{\hbar^2}{2mr^2} \frac{d^2}{d\phi^2} \]

Al sustituir el Hamiltoniano en la ecuación de Schrödinger, se obtiene

\[ -\frac{\hbar^2}{2mr^2} \frac{d^2}{d\phi^2} \psi = E \psi \]

La solución a la ecuación diferencial tiene la forma

\[ \psi = Ae^{im_l\phi} + Be^{-im_l\phi} \]

con \(m_l = ( 2mr^2 E/\hbar^2 )^{1/2}\). Despejando se obtiene que

\[ E = \frac{\hbar^2 m_l^2}{2mr^2} \]

Inserto matemático: Condiciones a la frontera

Debido a que la eigenfunción debe ser contínua, y a que la partícula se mueve en un anillo, debe de cumplirse la condición cíclica \(\psi(\phi) = \psi(\phi+2\pi)\), es decir que al dar una vuelta, la eigenfunción debe terminar en el mismo punto donde comenzó. Sustituyendo la eigenfunción en la condición cíclica se obtiene

\[ Ae^{im_l\phi} + Be^{-im_l\phi} = Ae^{im_l\phi}e^{im_l2\pi} + Be^{-im_l\phi}e^{-im_l2\pi} \]

Para que la igualdad anterior pueda cumplirse, \(m_l\) debe ser un número entero, tal que se cumpla \(e^{im_l2\pi}=e^{-im_l2\pi}=1\). Esto origina la cuantización \(m_l = {0, \pm 1, \pm 2, \cdots}\).

Tras aplicar las condiciones a la frontera, normalizar y con B=0,

\[ \psi = \left( \frac{1}{2\pi} \right)^{1/2} e^{i m_l \phi} = \left( \frac{1}{2\pi} \right)^{1/2} \cos(m_l \phi) + i \left( \frac{1}{2\pi} \right)^{1/2} \sin(m_l \phi) \]

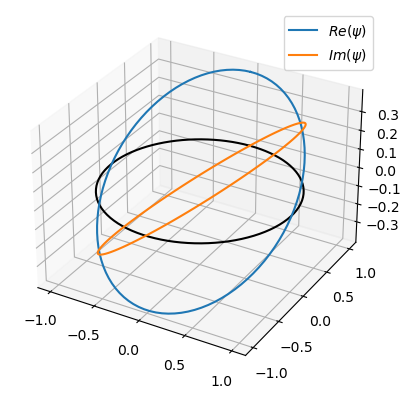
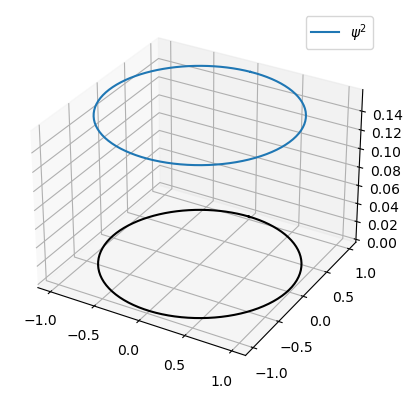
Grafique la eigenfunción y su cuadrado para \(m_l=1\)

# Gráfica

# Gráfica

import numpy as np
import matplotlib.pyplot as plt

#Número cuántico
ml=1

#Coordenadas polares
phi = np.linspace(0, 2 * np.pi, 100)
r=1.0
psi_r = np.sqrt(1/(2*np.pi))*np.cos(ml*phi)
psi_i = np.sqrt(1/(2*np.pi))*np.sin(ml*phi)

#Gráfica de la eigenfunción
ax = plt.axes(projection='3d')
x = r * np.sin(phi)
y = r * np.cos(phi)
ax.plot(x, y, 0, color='k') #Eje de la gráfica
ax.plot(x, y, psi_r, label='$Re(\psi)$')
ax.plot(x, y, psi_i, label='$Im(\psi)$')
ax.legend()
plt.show()

#Gráfica del cuadrado de la eigenfunción
ax = plt.axes(projection='3d')
x = r * np.sin(phi)
y = r * np.cos(phi)
ax.plot(x, y, 0, color='k') #Eje de la gráfica
ax.plot(x, y, ((psi_r+1J*psi_i)*(psi_r-1J*psi_i)).real, label='$\psi^2$')
ax.legend()
plt.show()
_images/Anillo_4_0.png _images/Anillo_4_1.png

7.1. Referencias#

  • B.D. Anderson, Cyclic Polyynes as Examples of the Quantum Mechanical Particle on a Ring, J. Chem. Educ. 89, 724 (2012).

  • M.A.R.B. Castanho, Teaching Molecular Applications of the Particle-in-a-Ring Model Using Azulene, J. Chem. Educ. 79, 1092 (2002).

  • A. Vincent, An Alternative Derivation of the Energy Levels of the “Particle on a Ring” System, J. Chem. Educ. 73, 1001 (1996).

  • M.D. Ellison, The Particle inside a Ring: A Two-Dimensional Quantum Problem Visualized by Scanning Tunneling Microscopy, J. Chem. Educ. 85, 1282 (2008).

  • P. W. Atkins, y R. Friedman, Molecular Quantum Mechanics (Oxford University Press, 2005).

  • D.A. McQuarrie y J.D. Simon, Physical Chemistry: A Molecular Approach (University Science Books, 1997).