8. Partícula en la esfera#

Se tiene una partícula moviéndose sobre una superficie esférica de radio constante.

La ecuación de Schrödinger a resolver es

\[ -\frac{\hbar^2}{2m} \nabla^2 \psi(\theta,\phi) = E \psi(\theta,\phi) \]

Inserto matemático: Hamiltoniano

Donde

\[ \nabla^2 = \frac{1}{r} \frac{\partial^2}{\partial r^2}r + \frac{1}{r^2} \Lambda^2 = \frac{1}{r} \frac{\partial^2}{\partial r^2} r + \frac{1}{r^2} \left( \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} + \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} \right) \]

Si r es constante, entonces

\[ -\frac{\hbar^2}{2mr^2} \Lambda^2 \psi(\theta,\phi) = E \psi(\theta,\phi) \]

Las soluciones de esta ecuación son los armónicos esféricos.

Inserto matemático: Armónicos esféricos

Los armónicos esféricos se definen por

\[ Y_l^{m_l}(\theta,\phi) = \sqrt{\frac{2l+1}{4\pi} \frac{(l-|m_l|)!}{(l+|m_l|)!}} e^{i m_l \phi} P_l^{m_l}(\cos(\theta)) \]

donde \(P_l^{m_l}(\cos(\phi))\) son los polinomios asociados de Legendre, dados por

\[ P_l^{m_l}(x) = \frac{l}{2^l l!}(1-x^2)^{|m_l|/2} \frac{d^{l+|m_l|}}{dx^{l+|m_l|}} (x^2-1)^l \]

En la tabla se muestra la forma de los primeros armónicos esféricos. En este punto han aparecido dos números cuánticos, tal que \(l = 0,1,2,3,...\) y \(m_l = -l, -l+1, 0, l-1, l\)

\(l\)	\(m_l\)	Armónico esférico \(Y_l^{m_l}(\theta,\phi)\)
0	0	\(\frac{1}{(4\pi)^{1/2}}\)
1	-1	\(+\frac{3}{(8\pi)^{1/2}} \sin \theta e^{-i\phi}\)
1	0	\(\frac{3}{(4\pi)^{1/2}} \cos \theta\)
1	1	\(-\frac{3}{(8\pi)^{1/2}} \sin \theta e^{i\phi}\)
2	-2	\(+\frac{15}{(32\pi)^{1/2}} \sin^2 \theta e^{-2i\phi}\)
2	-1	\(+\frac{15}{(8\pi)^{1/2}} \sin \theta \cos \theta e^{-i\phi}\)
2	0	\(\frac{5}{(16\pi)^{1/2}} (3\cos^2 \theta - 1)\)
2	1	\(-\frac{15}{(8\pi)^{1/2}} \sin \theta \cos \theta e^{i\phi}\)
2	2	\(-\frac{15}{(32\pi)^{1/2}} \sin^2 \theta e^{2i\phi}\)

La energía del sistema está dada por

\[ E = -l(l+1) \]

Grafique el armónico esférico \(|Y_1^{0}|\) y su cuadrado.

# Gráfica

#Gráfica

import scipy.special as sp
import numpy as np
import matplotlib.pyplot as plt

ml=0
l=1

theta = np.linspace(0,np.pi,100)
phi = np.linspace(0,2*np.pi,100)
THETA,PHI=np.meshgrid(theta,phi)

R=np.abs(sp.sph_harm(ml,l,PHI,THETA))

X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z,cmap='YlOrRd')
#ax.set_xlim(-0.4,0.4)
#ax.set_ylim(-0.4,0.4)
#ax.set_zlim(-0.4,0.4)
ax.set_title("$\Psi$")
plt.show()

R=np.power(R,2.0)

X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z,cmap='YlOrRd')
ax.set_xlim(-0.2,0.2)
ax.set_ylim(-0.2,0.2)
ax.set_zlim(-0.2,0.2)
ax.set_title("$\Psi^2$")
plt.show()

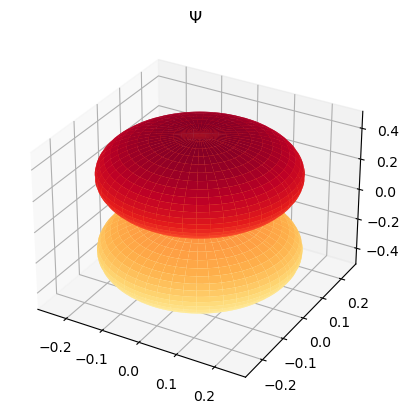
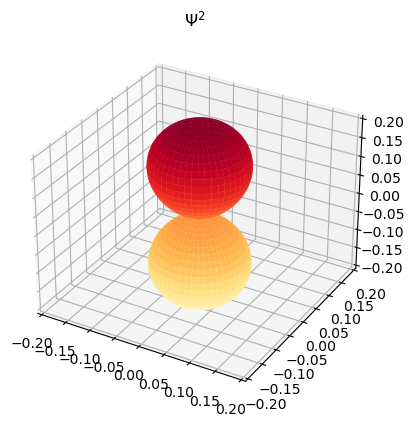
8.1. Referencias#

A.J.C. Varandas y L.J.A. Martins, On the stability of a hydrogen-like atom: The particle in a spherical box revisited, J. Chem. Educ. 63, 485 (1986).
P. W. Atkins, y R. Friedman, Molecular Quantum Mechanics (Oxford University Press, 2005).
I.N. Levine, D.H. Busch, y H. Shull, Quantum chemistry (Pearson Prentice Hall Upper Saddle River, NJ, 2009).
D.A. McQuarrie y J.D. Simon, Physical Chemistry: A Molecular Approach (University Science Books, 1997).

Cuántica I

Partícula en la esfera

Contents

8. Partícula en la esfera#

8.1. Referencias#