6. Efecto Túnel#

Considere una partícula moviéndose por la izquierda hacia una barrera de potencial de longitud finita con valor V en \(0 \leq x \leq L\), es decir:

\[\begin{split} V(x) = \left\{ \begin{array}{lll} 0 & \mathrm{si\ } x < 0 & \text{I}\\ V & \mathrm{si\ } 0 \leq x \leq L & \text{II} \\ 0 & \mathrm{si\ } L \le x & \text{III} \\ \end{array} \right. \end{split}\]

En este caso no hay cuantización, por lo que la partícula puede tomar cualquier valor de energía. Analizaremos dos casos particulares

La partícula tiene menor energía que el potencial \(E<V\).
La partícula tiene mayor energía que el potencial \(E>V\).

6.1. Energía menor que el potencial \(E < V\)#

Para pensar

De manera clásica, cuando la partícula tiene menor energía que el potencial, \(E<V\), no debería poder pasar a la región II ni a la región III. ¿Qué pasará cuánticamente?

El sistema puede analizarse por regiones

Inserto matemático: Hamiltoniano por regiones

Región	Hamiltoniano	Eigenfunción	Constantes
\({\rm I}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)	\(\psi_{\rm I}(x) = Ae^{ik_1x} + Be^{-ik_1x}\)	\(k_1^2 = \frac{2mE}{\hbar^2}\)
\({\rm II}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V\)	\(\psi_{\rm II}(x) = C e^{-k_2x} + De^{k_2x}\)	\(k_2^2 = \frac{2m(V-E)}{\hbar^2}\)
\({\rm III}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)	\(\psi_{\rm III}(x) = Fe^{ik_1x} + Ge^{-ik_1x}\)	\(k_1^2 = \frac{2mE}{\hbar^2}\)

Los coeficientes pueden obtenerse a partir de la condición de continuidad de la eigenfunción en \(x=0\) y \(x=L\)

Inserto matemático: Condiciones de continuidad

Regiones	Condición	Ecuación
\({\rm I}\) y \({\rm II}\)	\(\psi_{\rm I}(0) = \psi_{\rm II}(0)\)	\(A + B = C + D\)
\({\rm I}\) y \({\rm II}\)	\(\frac{d\psi_{\rm I}}{dx}(0) = \frac{d\psi_{\rm II}}{dx}(0)\)	\(ik_1 (A - B) = -k_2 (C - D)\)
\({\rm III}\)	La partícula viaja hacia la derecha	\(G = 0\)
\({\rm II}\) y \({\rm III}\)	\(\psi_{\rm II}(L) = \psi_{\rm III}(L)\)	\(Ce^{-k_2L} + De^{k_2L} = F e^{ik_1L}\)
\({\rm II}\) y \({\rm III}\)	\(\frac{d\psi_{\rm II}}{dx}(L) = \frac{d\psi_{\rm III}}{dx}(L)\)	\(-k_2 C e^{-k_2L} + k_2 D e^{k_2L} = ik_1F e^{ik_1L}\)

Al despejar, se obtiene

\[ C = \frac{F}{2} \left( 1 - \frac{i k_1}{k_2} \right) e^{ik_1L + k_2L} \]

\[ D = \frac{F}{2} \left( 1 + \frac{i k_1}{k_2} \right) e^{ik_1L - k_2L} \]

\[ A = \frac{1}{2} \left[ \left(1 + \frac{i k_2}{k_1} \right)C + \left(1 - \frac{i k_2}{k_1} \right)D \right] \]

El coeficiente de transmisión se puede calcular al dividir el cuadrado del coeficiente de la parte de la función que representa el paso de partículas a la región \({\rm III}\) (coeficiente \(F\)), entre el cuadrado del coeficiente de la parte de la eigenfunción que representa a la partícula dirigiéndose hacia la región \({\rm I}\) (coeficiente \(A\)).

\[ T = \frac{|F|^2}{|A|^2} = \frac{16(E/V)(1-E/V)}{16(E/V)(1-E/V) + (e^{k_2L} - e^{-k_2L})^2} \]

Importe numpy y pyplot de matplotlib.

# Importe librerías

import numpy as np
from matplotlib import pyplot as plt

De valores a las constantes del sistema. Considere \(m=1\), \(\hbar=1\) y \(L=1\). Asigne un valor de energía y potencial respetando la relación \(E < V\), por ejemplo, \(E=1\), \(V=10\).

# m, hbar, L, E, V

m = 1
hbar = 1
L = 1
E = 1
V = 10

Defina \(k_1\) y \(k_2\) acorde a

\[ k_1 = \sqrt{\frac{2mE}{\hbar^2}} \]

\[ k_2 = \sqrt{\frac{2m(V-E)}{\hbar^2}} \]

#k1 y k2

k1 = np.sqrt(2*m*E/hbar**2)
k2 = np.sqrt(2*m*(V-E)/hbar**2)

A continuación graficaremos el cuadrado de la eigenfunción. Para ello, primero defina las siguientes constantes.

\[ C = \frac{F}{2} \left( 1 - \frac{i k_1}{k_2} \right) e^{ik_1L + k_2L} \]

\[ D = \frac{F}{2} \left( 1 + \frac{i k_1}{k_2} \right) e^{ik_1L - k_2L} \]

\[ A = \frac{1}{2} \left[ \left(1 + \frac{i k_2}{k_1} \right)C + \left(1 - \frac{i k_2}{k_1} \right)D \right] \]

\[ B = C + D - A \]

Considere

\[ F = 1 \]

# A, B, C, D, F

F = 1

C = F/2*(1 - 1j*k1/k2)*np.exp(1j*k1*L+k2*L)
D = F/2*(1 + 1j*k1/k2)*np.exp(1j*k1*L-k2*L)
A = 1/2*((1 + 1j*k1/k2)*C + (1 - 1j*k1/k2)*D)
B = C + D - A

Defina un dominio para \(x\). Sugerencia: Use numpy.linspace

# Dominio de x

x1 = np.linspace(-10,0,100)
x2 = np.linspace(0,L,100)
x3 = np.linspace(L,10,100)

Defina la eigenfunción en las tres regiones según

\[\begin{split} \psi(x) = \left\{ \begin{array}{lll} A e^{ik_1x}+ B e^{-ik_1x} & \mathrm{si\ } x < 0 & \text{I}\\ C e^{-k_2x} + De^{k_2x} & \mathrm{si\ } 0 \leq x \leq L & \text{II} \\ F e^{ik_1x}& \mathrm{si\ } L \le x & \text{III} \\ \end{array} \right. \end{split}\]

# psi_I, psi_II y psi_III

psi_I = A*np.exp(1j*k1*x1) + B*np.exp(-1j*k1*x1)
psi_II = C*np.exp(-k2*x2) + D*np.exp(k2*x2)
psi_III = F*np.exp(1j*k1*x3)

Grafique el cuadrado de la eigenfunción.

# Gráfica

plt.plot(x1,abs(psi_I)**2)
plt.plot(x2,abs(psi_II)**2)
plt.plot(x3,abs(psi_III)**2)

[<matplotlib.lines.Line2D at 0x14be382cf5e0>]

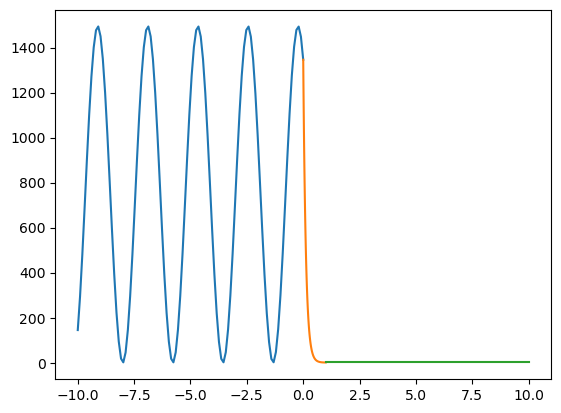
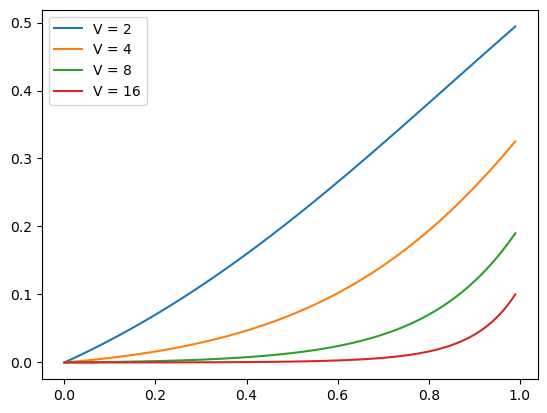
A continuación, calcule el coeficiente de transmisión a diferentes energías y diferentes potenciales, cumpliendo \(E<V\).

Para \(V=2,4,8,16\):

1 Defina un conjunto de 100 energías de 0 a V. Sugerencia. Use numpy.linspace.

2 Calcule \(k_2\)

\[ k_2^2 = \frac{2m(V-E)}{\hbar^2} \]

3 Calcule el coeficiente de transmisión. Recuerde

\[ T = \frac{16(E/V)(1-E/V)}{16(E/V)(1-E/V) + (e^{k_2L} - e^{-k_2L})^2} \]

4 Grafique T vs E/V

# Gráficas

for V in [2,4,8,16]:
    
    E = np.linspace(0,V,100,endpoint=False)
    k2 = np.sqrt(2*m*(V-E)/hbar**2)
    T = 16*(E/V)*(1-E/V)/(16*(E/V)*(1-E/V) + (np.exp(k2*L) - np.exp(-k2*L))**2)
    plt.plot(E/V,T,label="V = "+str(V))
    plt.legend()

6.2. Energía mayor que el potencial \(E > V\)#

Para pensar

De manera clásica, cuando la partícula tiene mayor energía que el potencial, \(E>V\), debería poder moverse sin ninguna restricción. ¿Qué pasará cuánticamente?

El sistema puede analizarse por regiones

Inserto matemático: Hamiltoniano por regiones

Región	Hamiltoniano	Eigenfunción	Constantes
\({\rm I}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)	\(\psi_I(x) = Ae^{ik_1x} + Be^{-ik_1x}\)	\(k_1^2 = \frac{2mE}{\hbar^2}\)
\({\rm II}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V\)	\(\psi_{II}(x) = C e^{ik_2x} + De^{-ik_2x}\)	\(k_2^2 = \frac{2m(E-V)}{\hbar^2}\)
\({\rm III}\)	\(- \frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)	\(\psi_{III}(x) = Fe^{ik_1x} + Ge^{-ik_1x}\)	\(k_1^2 = \frac{2mE}{\hbar^2}\)

Los coeficientes pueden obtenerse a partir de la condición de continuidad de la eigenfunción en \(x=0\) y \(x=L\)

Inserto matemático: Condiciones de continuidad

Regiones	Condición	Ecuación
\({\rm I}\) y \({\rm II}\)	\(\psi_{\rm I}(0) = \psi_{II}(0)\)	\(A + B = C + D\)
\({\rm I}\) y \({\rm II}\)	\(\frac{d\psi_{\rm I}}{dx}(0) = \frac{d\psi_{\rm II}}{dx}(0)\)	\(k_1 (A - B) = k_2 (C - D)\)
\({\rm III}\)	La partícula viaja hacia la derecha	\(G = 0\)
\({\rm II}\) y \({\rm III}\)	\(\psi_{\rm II}(L) = \psi_{III}(L)\)	\(Ce^{ik_2L} + De^{-k_2L} = F e^{ik_1L}\)
\({\rm II}\) y \({\rm III}\)	\(\frac{d\psi_{\rm II}}{dx}(L) = \frac{d\psi_{\rm III}}{dx}(L)\)	\(k_2 \left( C e^{ik_2L} + D e^{-ik_2L} \right) = k_1F e^{ik_1L}\)

Al despejar, se obtiene

\[ C = \frac{F}{2} \left( 1 + \frac{k_1}{k_2} \right) e^{i(k_1-k_2)L} \]

\[ D = \frac{F}{2} \left( 1 - \frac{k_1}{k_2} \right) e^{i(k_1+k_2)L} \]

\[ A = \frac{1}{2} \left[ \left(1 + \frac{k_2}{k_1} \right)C + \left(1 - \frac{k_2}{k_1} \right)D \right] \]

\[ T = \frac{4(E/V)(E/V-1)}{4(E/V)(E/V-1) + \sin^2(k_2L)} \]

De valores a las constantes del sistema. Considere \(m=1\), \(\hbar=1\) y \(L=1\). Asigne un valor de energía y potencial respetando la relación \(E > V\), por ejemplo, \(E=40\), \(V=10\).

# m, hbar, L, E, V

m = 1
hbar = 1
L = 1
E = 40
V = 10

Defina \(k_1\) y \(k_2\) acorde a

\[ k_1 = \sqrt{\frac{2mE}{\hbar^2}} \]

\[ k_2 = \sqrt{\frac{2m(E-V)}{\hbar^2}} \]

#k1 y k2

k1 = np.sqrt(2*m*E/hbar**2)
k2 = np.sqrt(2*m*(E-V)/hbar**2)

A continuación graficaremos el cuadrado de la eigenfunción. Para ello, primero defina las siguientes constantes.

\[ C = \frac{F}{2} \left( 1 + \frac{k_1}{k_2} \right) e^{i(k_1-k_2)L} \]

\[ D = \frac{F}{2} \left( 1 - \frac{k_1}{k_2} \right) e^{i(k_1+k_2)L} \]

\[ A = \frac{1}{2} \left[ \left(1 + \frac{k_2}{k_1} \right)C + \left(1 - \frac{k_2}{k_1} \right)D \right] \]

\[ B = C + D - A \]

Considere

\[ F = 1 \]

# A, B, C, D, F

F = 1

C = F/2*(1 + k1/k2)*np.exp(1j*(k1-k2)*L)
D = F/2*(1 - k1/k2)*np.exp(1j*(k1+k2)*L)
A = 1/2*((1 + k2/k1)*C + (1 - k2/k1)*D)
B = C + D - A

Defina un dominio para \(x\). Sugerencia: Use numpy.linspace

# Dominio de x

x1 = np.linspace(-2,0,100)
x2 = np.linspace(0,L,100)
x3 = np.linspace(L,2,100)

Defina la eigenfunción en las tres regiones según

\[\begin{split} \psi(x) = \left\{ \begin{array}{lll} A e^{ik_1x}+ B e^{-ik_1x} & \mathrm{si\ } x < 0 & I\\ C e^{ik_2x} + De^{-ik_2x} & \mathrm{si\ } 0 \leq x \leq L & II \\ F e^{ik_1x}& \mathrm{si\ } L \le x & III \\ \end{array} \right. \end{split}\]

# psi_I, psi_II y psi_III

psi_I = A*np.exp(1j*k1*x1) + B*np.exp(-1j*k1*x1)
psi_II = C*np.exp(1j*k2*x2) + D*np.exp(-1j*k2*x2)
psi_III = F*np.exp(1j*k1*x3)

Grafique el cuadrado de la eigenfunción.

# Grafica

plt.plot(x1,abs(psi_I)**2)
plt.plot(x2,abs(psi_II)**2)
plt.plot(x3,abs(psi_III)**2)

[<matplotlib.lines.Line2D at 0x14be29694c70>]

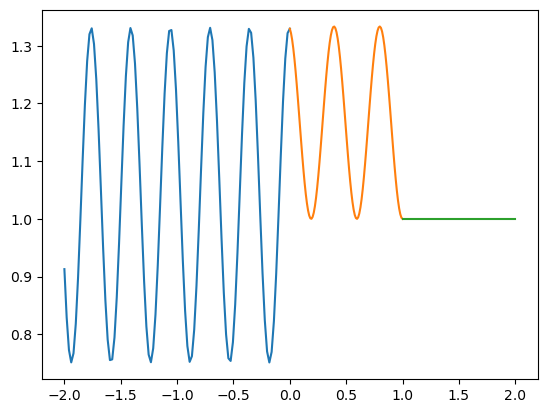
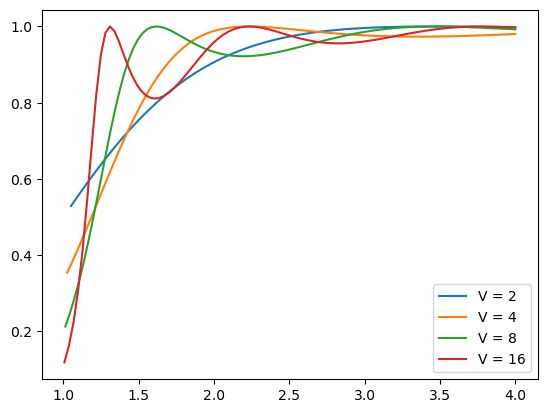
Para \(V=2,4,8,16\):

1 Defina un conjunto de 100 energías de V a 4V. Sugerencia. Use numpy.linspace.

2 Calcule \(k_2\)

3 Calcule el coeficiente de transmisión. Recuerde

4 Grafique T vs E/V

# Gráfica

for V in [2,4,8,16]:
    
    E = np.linspace(V+0.1,4*V,100)
    k2 = np.sqrt(2*m*(E-V)/hbar**2)
    T = 4*(E/V)*(E/V-1)/(4*(E/V)*(E/V-1) + (np.sin(k2*L))**2)
    plt.plot(E/V,T,label="V = "+str(V))
    plt.legend()

Reto para aprender más

Para ver una combinación del efecto túnel debido a una barrera de potencial a la mitad de la caja puede revisar el Notebook de Efecto Túnel en la Caja.

Cuántica I

Efecto Túnel

Contents

6. Efecto Túnel#

6.1. Energía menor que el potencial \(E < V\)#

6.2. Energía mayor que el potencial \(E > V\)#