12. Orbitales Atómicos#

Para la parte angular se tiene la ecuación de valores propios

\[ \Lambda^2 Y_l^{m_l} = -l(l+1)\hbar^2 Y_l^{m_l} \]

donde \(\Lambda^2\) es el Legendriano.

Inserto matemático: Legendriano

El Legendriano \(\Lambda^2\) se define por

\[ \Lambda^2 = \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} + \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \sin \theta \frac{\partial}{\partial \theta} \]

La solución a la parte angular son los armónicos esféricos \(Y_l^{m_l}(\theta,\phi)\).

Note que \(l\) y \(m_l\) son números cuánticos que deben cumplir:

\[ l = 0,1,2,3,... \]

\[ m_l = -l,-l+1,...,0,...,l-1,l \]

En la tabla se muestran los primeros armónicos esféricos.

\(l\)	\(m_l\)	Armónico esférico \(Y_l^{m_l}(\theta,\phi)\)
0	0	\(\frac{1}{(4\pi)^{1/2}}\)
1	-1	\(+\frac{3}{(8\pi)^{1/2}} \sin \theta e^{-i\phi}\)
1	0	\(\frac{3}{(4\pi)^{1/2}} \cos \theta\)
1	1	\(-\frac{3}{(8\pi)^{1/2}} \sin \theta e^{i\phi}\)
2	-2	\(\frac{15}{(32\pi)^{1/2}} \sin^2 \theta e^{-2i\phi}\)
2	-1	\(+\frac{15}{(8\pi)^{1/2}} \sin \theta \cos \theta e^{-i\phi}\)
2	0	\(\frac{5}{(16\pi)^{1/2}} (3\cos^2 \theta - 1)\)
2	1	\(-\frac{15}{(8\pi)^{1/2}} \sin \theta \cos \theta e^{i\phi}\)
2	2	\(\frac{15}{(32\pi)^{1/2}} \sin^2 \theta e^{2i\phi}\)

Importe las siguientes librerías

numpy
pyplot de matplotlib
special de scipy

# Librerías

#%matplotlib notebook
from scipy import special
import numpy as np
from matplotlib import pyplot as plt

Definimos un mallado que considere \(\theta \in [0,\pi]\) y \(\phi\in[0,2\pi]\)

La idea es pensar en graficar una figura en tres dimensiones y que necesitaremos todas las combinaciones de todos los valores de \(\theta\) y \(\phi\)

Aprendizaje de código

Utilice las siguientes instrucciones

theta = np.linspace(0,np.pi,200)
phi = np.linspace(0,2*np.pi,200)
THETA,PHI = np.meshgrid(theta,phi)

# Mallado

theta = np.linspace(0,np.pi,200)
phi = np.linspace(0,2*np.pi,200)
THETA,PHI = np.meshgrid(theta,phi)

Seleccione un valor de \(l\) y \(m_l\)

Note

se recomienda \(l=1\) y \(m_l=1\) para empezar, pero puede probar con otros

# Seleccione l y ml

l = 1
ml = 1

A continuación graficaremos armónicos esféricos y su cuadrado.

Aprendizaje de código

Copie y pegue el siguiente código

R = abs(special.sph_harm(ml,l,PHI,THETA))
R = R**2

X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)

fig = plt.figure()

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z,cmap='cividis')
ax.set_xlim(-R.max(),R.max())
ax.set_ylim(-R.max(),R.max())
ax.set_zlim(-R.max(),R.max())

ax.set_title("$Y^2$"+" l="+str(l)+" ml="+str(ml))

plt.show()

# Gráfica

R = abs(special.sph_harm(ml,l,PHI,THETA))
R = R**2

X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)

fig = plt.figure()

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z,cmap='cividis')
ax.set_xlim(-R.max(),R.max())
ax.set_ylim(-R.max(),R.max())
ax.set_zlim(-R.max(),R.max())

ax.set_title("$Y^2$"+" l="+str(l)+" ml="+str(ml))

plt.show()

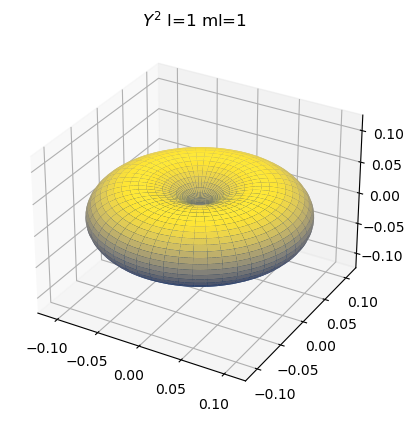
Recordemos que la eigenfunción es el producto de una parte radial y una parte angular \(\psi_{n,l,m_l}=R_{n,l}(r)Y_l^{m_l}(\theta,\phi)\)

Nombraremos a los orbitales p como:

\[\begin{split} \color{green}{p_z} &=& R_{n1} \color{blue}{Y_{1}^{0}} = R_{n1} \left(\frac{3}{4 \pi}\right)^{1/2} \cos \theta \\ \color{green}{p_-} &=& R_{n1} \color{blue}{Y_{1}^{-1}} = R_{n1} \left(\frac{3}{8 \pi}\right)^{1/2} \sin \theta \color{red}{e^{-i\phi}}\\ \color{green}{p_+} &=& R_{n1} \color{blue}{Y_{1}^{+1}} = -R_{n1} \left(\frac{3}{8 \pi}\right)^{1/2} \sin \theta \color{red}{e^{i\phi}} \end{split}\]

El orbital \(p_z\) es real, pero \(p_-\) y \(p_+\) son complejos. Recordando la fórmula de Euler:

\[\begin{split} e^{-i\phi} &=& \cos(\phi) - i \sin(\phi)\\ -e^{i\phi} &=& -\cos(\phi) - i \sin(\phi) \end{split}\]

Hacemos la combinación lineal:

\[\begin{split} \color{purple}{p_x} &=& \frac{1}{\sqrt{2}}(\color{green}{p_-} - \color{green}{p_+}) = R_{n1} \left(\frac{3}{4 \pi}\right)^{1/2} \sin \theta \cos \phi \\ \color{purple}{p_y} &=& \frac{i}{\sqrt{2}}(\color{green}{p_-} + \color{green}{p_+}) = R_{n1} \left(\frac{3}{4 \pi}\right)^{1/2} \sin \theta \sin \phi \end{split}\]

Represente la parte angular de las combinaciones lineales de \(p_-\) y \(p_+\) para formar \(p_x\) y \(p_y\).

# px y py

Rz = special.sph_harm(0,1,PHI,THETA)
R_m = special.sph_harm(-1,1,PHI,THETA)
R_p = special.sph_harm(+1,1,PHI,THETA)

R_x = (R_m-R_p)/np.sqrt(2)
R_y = 1j*(R_m+R_p)/np.sqrt(2)

R = abs(R_y)
orb_name = "py"
R = R**2

X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)

fig = plt.figure()

ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, cmap='cividis')
ax.set_xlim(-R.max(),R.max())
ax.set_ylim(-R.max(),R.max())
ax.set_zlim(-R.max(),R.max())
ax.set_title("$Y^2$"+orb_name)

plt.show()

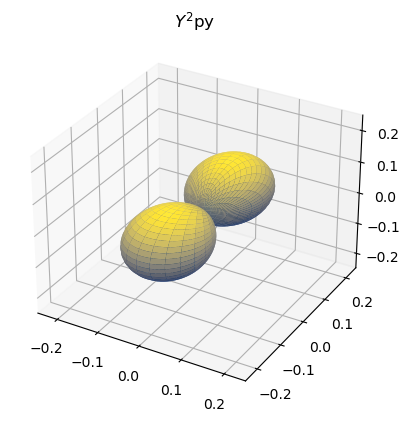
A continuación se dan las expresiones de algunos orbitales

Orbital	Eigenfunción
\(1s\)	\(N_1 e^{-r}\)
\(2s\)	\(N_2 (2-r)e^{-r/2}\)
\(2p_x\)	\(N_2 r \sin\theta \cos\phi e^{-r/2}\)
\(2p_y\)	\(N_2 r \sin\theta \sin\phi e^{-r/2}\)
\(2p_z\)	\(N_2 r \cos\theta e^{-r/2}\)

donde \(N_1\) y \(N_2\) son factores de normalización.

12.1. Referencias#

J. Autschbach, Orbitals: Some Fiction and Some Facts, J. Chem. Educ. 89, 1032 (2012).
P.C. Hiberty, F. Volatron, y S. Shaik, In Defense of the Hybrid Atomic Orbitals, J. Chem. Educ. 89, 575 (2012).
M. Labarca y O. Lombardi, Why orbitals do not exist?, Foundations of Chemistry 12, 149 (2010).
F.W. Eagle, K.D. Seaney, y M.P. Grubb, Musical Example To Visualize Abstract Quantum Mechanical Ideas, J. Chem. Educ. 94, 1989 (2017).
P. W. Atkins, y R. Friedman, Molecular Quantum Mechanics (Oxford University Press, 2005).
F.L. Pilar, Elementary Quantum Chemistry (Dover ed., 2001).
I.N. Levine, D.H. Busch, y H. Shull, Quantum chemistry (Pearson Prentice Hall Upper Saddle River, NJ, 2009).
D.A. McQuarrie y J.D. Simon, Physical Chemistry: A Molecular Approach (University Science Books, 1997).

Cuántica I

Orbitales Atómicos

Contents

12. Orbitales Atómicos#

12.1. Referencias#